Waves | Physics - Vibrations of Air Column | 11th Physics : UNIT 11 : Waves
Chapter: 11th Physics : UNIT 11 : Waves
Vibrations of Air Column
VIBRATIONS
OF AIR COLUMN
Musical
instruments like flute, clarinet, nathaswaram, etc are known as wind
instruments. They work on the principle of vibrations of air columns. The
simplest form of a wind instrument is the organ pipe. It is made up of a wooden
or metal pipe which produces the musical sound. For example, flute, clarinet
and nathaswaram are organ pipe instruments. Organ pipe instruments are
classified into two types:
(a) Closed organ pipes:
Look at the picture of a clarinet, shown in Figure 11.36. It is a pipe with one end closed and the other end open. If one end of a pipe is closed, the wave reflected at this closed end is 180° out of phase with the incoming wave. Thus there is no displacement of the particles at the closed end. Therefore, nodes are formed at the closed end and anti-nodes are formed at open end.
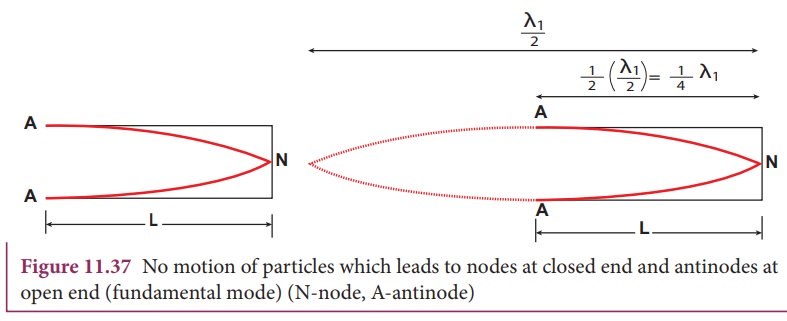
Let
us consider the simplest mode of vibration of the air column called the
fundamental mode. Anti-node is formed at the open end and node at closed end.
From the Figure 11.37, let L be the
length of the tube and the wavelength of the wave produced. For the fundamental
mode of vibration, we have,

which
is called the fundamental note.
The frequencies higher than
fundamental frequency can be produced by blowing air strongly at open end. Such
frequencies are called overtones.
The
Figure 11.38 shows the second mode of vibration having two nodes and two
anti-nodes, for which we have, from example 11.20.
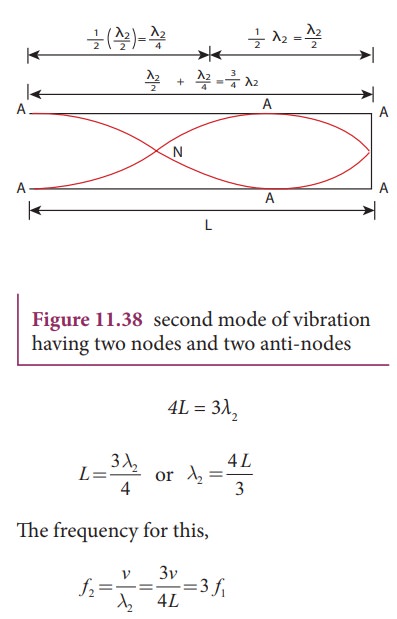
is
called first over tone, since here,
the frequency is three times the fundamental frequency it is called third harmonic.
The
Figure 11.39 shows third mode of vibration having three nodes and three
anti-nodes.
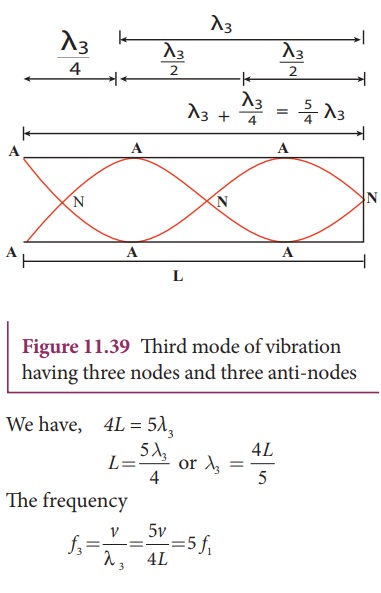
is
called second over tone, and since n = 5 here, this is called fifth harmonic. Hence, the closed
organ pipe has only odd harmonics and frequency of the nth harmonic is fn = (2n+1)f1. Therefore, the frequencies
of harmonics are in the ratio

(b) Open organ pipes:

Consider
the picture of a flute, shown in Figure 11.40. It is a pipe with both the ends
open. At both open ends, anti-nodes are formed. Let us consider the simplest
mode of vibration of the air column called fundamental mode. Since anti-nodes
are formed at the open end, a node is formed at the mid-point of the pipe.
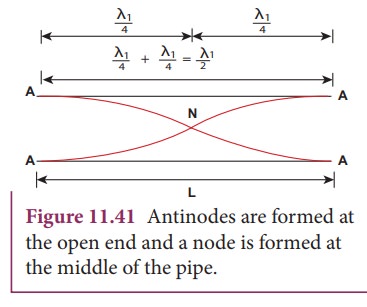
From
Figure 11.41, if L be the length of
the tube, the wavelength of the wave produced is given by

which
is called the fundamental note.
The
frequencies higher than fundamental frequency can be produced by blowing air
strongly at one of the open ends. Such frequencies are called overtones.
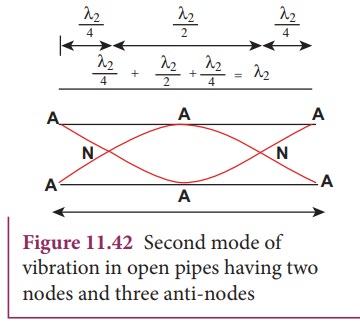
The Figure 11.42 shows the second mode of vibration in open
pipes. It has two nodes and three anti-nodes, and therefore,
L =λ2 or
λ2 = L
The
frequency

is
called first over tone. Since n
= 2 here, it is called the second harmonic.
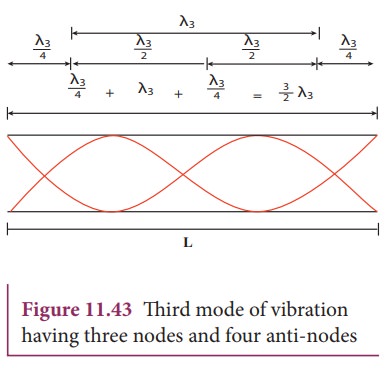
The
Figure 11.43 above shows the third mode of vibration having three nodes and
four anti-nodes

is
called second over tone. Since n = 3 here, it is called the third harmonic.
Hence,
the open organ pipe has all the harmonics and frequency of nth harmonic is fn = nf1. Therefore, the
frequencies of harmonics are in the ratio
f1 : f2 : f3 : f4 :…= 1 : 2 : 3 : 4 : … 11.79
EXAMPLE 11.25
If
a flute sounds a note with 450Hz ,
what are the frequencies of the second, third, and fourth harmonics of this
pitch?. If the clarinet sounds with a same note as 450Hz, then what are the frequencies of the lowest three harmonics
produced ?.
Solution
For
a flute which is an open pipe, we have
Second
harmonics f2 = 2 f1
= 900 Hz
Third
harmonics f3 = 3 f1 = 1350 Hz
Fourth
harmonics f4 = 4 f1 = 1800 Hz
For
a clarinet which is a closed pipe, we have
Second
harmonics f 2 = 3 f1 = 1350 Hz
Third
harmonics f 3 = 5 f1 = 2250 Hz
Fourth
harmonics f 4 = 7 f1 = 3150 Hz
EXAMPLE 11.26
If
the third harmonics of a closed organ pipe is equal to the fundamental
frequency of an open organ pipe, compute the length of the open organ pipe if
the length of the closed organ pipe is 30 cm.
Solution
Let
l2 be the length of the
open organ pipe, with l1
=30 cm the length of the closed organ
pipe.
It
is given that the third harmonic of closed organ pipe is equal to the
fundamental frequency of open organ pipe.
The
third harmonic of a closed organ pipe is
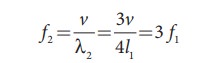
The
fundamental frequency of open organ pipe is
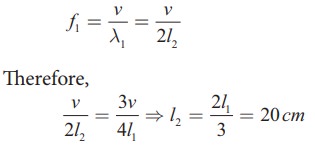
Related Topics