Terms and Definitions Used in Wave Motion

TERMS AND DEFINITIONS USED IN WAVE MOTION

Suppose we have two waves as shown in Figure 11.8. Are these two waves identical?. No. Though, the two waves are both sinusoidal, there are many difference between them. Therefore, we have to define some basic terminologies to distinguish one wave from another.

Consider a wave produced by a stretched string as shown in Figure 11.9.

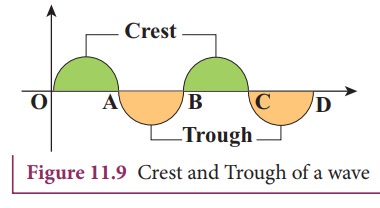
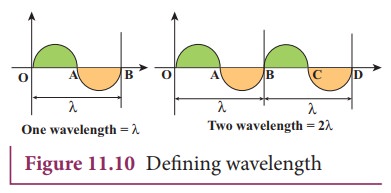
If we are interested in counting the number of waves created, let us put a reference level (mean position) as shown in Figure 11.9. Here the mean position is the horizontal line shown. The highest point in the shaded portion is called crest. With respect to the reference level, the lowest point on the un-shaded portion is called trough. This wave contains repetition of a section O to B and hence we define the length of the smallest section without repetition as one wavelength as shown in Figure 11.10. In Figure 11.10 the length OB or length BD is one wavelengh. A Greek letter lambda λ is used to denote one wavelength.

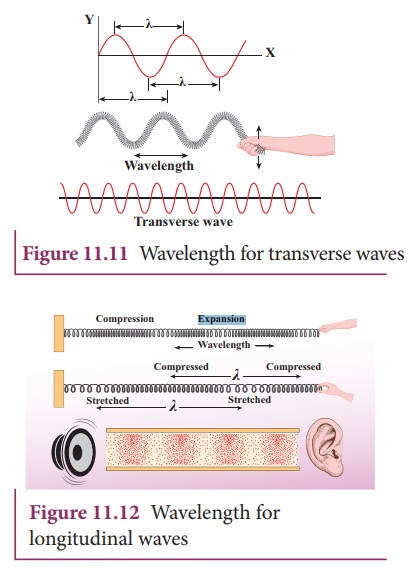
For transverse waves (as shown in Figure 11.11), the distance between two neighbouring crests or troughs is known as the wavelength.

For longitudinal waves, (as shown in Figure 11.12) the distance between two neighbouring compressions or rarefactions is known as the wavelength. The SI unit of wavelength is meter.

EXAMPLE 11.1

Which of the following has longer wavelength?

Answer is (c) 

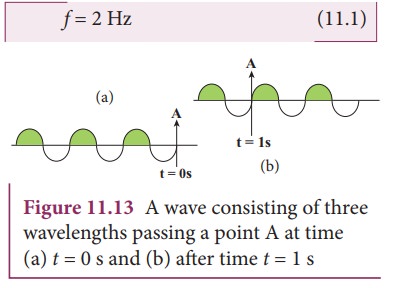
In order to understand frequency and time period, let us consider waves (made of three wavelengths) as shown in Figure 11.13 (a). At time t = 0 s, the wave reaches the point A from left. After time t = 1 s (shown in figure 11.13(b)), the number of waves which have crossed the point A is two. Therefore, the frequency is defined as “the number of waves crossing a point per second” It is measured in hertz whose symbol is Hz. In this example,

If two waves take one second (time) to cross the point A then the time taken by one wave to cross the point A is half a second. This defines the time period T as

From equation (11.1) and equation (11.2), frequency and time period are inversely related i.e.,

Time period is defined as the time taken by one wave to cross a point.

EXAMPLE 11.2

Three waves are shown in the figure below

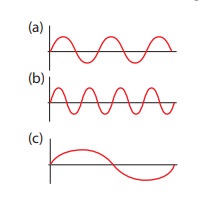
Write down 

(a) the frequency in ascending order

(b) the wavelength in ascending order

Solution

(a) f_c < f_a < f_b

(b) λ_b < λ_a < λ_c

From the example 11.2, we observe that the frequency is inversely related to the wavelength, f ∝ 1/λ

Then, fλ is equal to what?

[(i.e) fλ=?]

A simple dimensional argument will help us to determine this unknown physical quantity.

Dimension of wavelength is, [λ] = L

Frequency f = 1/ Time period , which implies that the dimension of frequency is,

where v is known as the wave velocity or phase velocity. This is the velocity with which the wave propagates. Wave velocity is the distance travelled by a wave in one second.

Note:

1. The number of cycles (or revolutions) per unit time is called angular frequency. Angular frequency, ω = 2π/T = 2πf (unit is radians/second)

2. The number of cycles per unit distance or number of waves per unit distance is called wave number.

wave number, k = 2π/λ (unit is radians/ meter)

In two, three or higher dimensional case, the wave number is the magnitude of a vector called wave vector. The points in space of wave vectors are called reciprocal vectors,  .

Dimensions of  is L^-1.

The velocity v, angular frequency ω and wave number λ are related as:

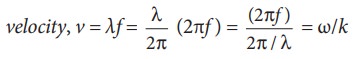
Wave numbers and wave vectors play an essential role in optics and scattering theory.

EXAMPLE 11.3

The average range of frequencies at which human beings can hear sound waves varies from 20 Hz to 20 kHz. Calculate the wavelength of the sound wave in these limits. (Assume the speed of sound to be 340 m s^-1.

Solution

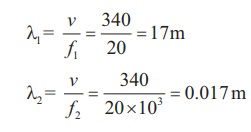
Therefore, the audible wavelength region is from 0.017 m to 17 m when the velocity of sound in that region is 340 m s^-1.

EXAMPLE 11.4

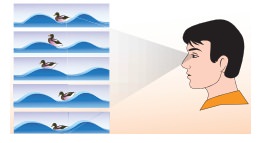
A man saw a toy duck on a wave in an ocean. He noticed that the duck moved up and down 15 times per minute. He roughly measured the wavelength of the ocean wave as 1.2 m. Calculate the time taken by the toy duck for going one time up and down and also the velocity of the ocean wave.

Solution

Given that the number of times the toy duck moves up and down is 15 times per minute. This information gives us frequency (the number of times the toy duck moves up and down)

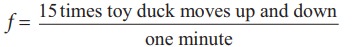
But one minute is 60 second, therefore, expressing time in terms of second

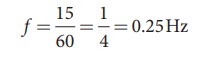
The time taken by the toy duck for going one time up and down is time period which is inverse of frequency

The velocity of ocean wave is v

v = λf = 1.2 ×0.25 = 0.3 m s^-1.

Amplitude of a wave:

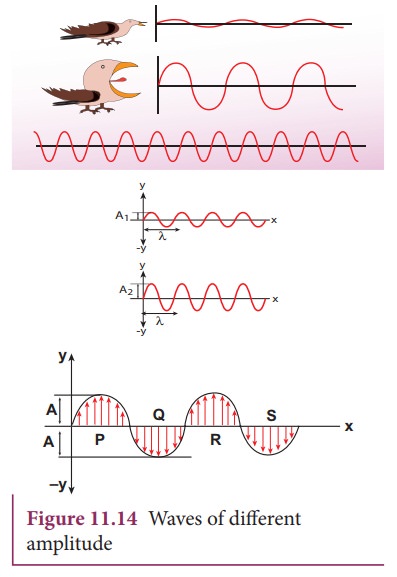
The waves shown in the Figure 11.14 have same wavelength, same frequency and same time period and also move with same velocity. The only difference between two waves is the height of either crest or trough. This means, the height of the crest or trough also signifies a wave character. So we define a quantity called an amplitude of the wave, as the maximum displacement of the medium with respect to a reference axis (for example in this case x-axis). Here, it is denoted by A.

EXAMPLE 11.5

Consider a string whose one end is attached to a wall. Then compute the following in both situations given in figure (assume waves crosses the distance in one second)

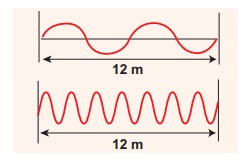
(a)  Wavelength,

(b)  Frequency and 

(c)  Velocity

Solution

This means that the speed of the wave along a string is a constant. Higher the frequency, shorter the wavelength and vice versa, and their product is velocity which remains the same.