Physics - Oscillations: Important Questions | 11th Physics : UNIT 10 : Oscillations
Chapter: 11th Physics : UNIT 10 : Oscillations
Oscillations: Important Questions
OSCILLATIONS
Short Answers Questions
1. What is meant by
periodic and non- periodic motion?. Give any two examples, for each motion.
2. What is meant by
force constant of a spring?.
3. Define time period
of simple harmonic motion.
4. Define frequency of
simple harmonic motion.
5. What is an epoch?.
6. Write short notes on
two springs connected in series.
7. Write short notes on
two springs connected in parallel.
8. Write down the time
period of simple pendulum.
9. State the laws of simple
pendulum?.
10. Write down the
equation of time period for linear harmonic oscillator.
11. What is meant by
free oscillation?.
12. Explain damped
oscillation. Give an example.
13. Define forced
oscillation. Give an example.
14. What is meant by
maintained oscillation?. Give an example.
15. Explain resonance.
Give an example.
Long Answers Questions
1. What is meant by
simple harmonic oscillation?. Give examples and explain why every simple
harmonic motion is a periodic motion whereas the converse need not be true.
2. Describe Simple
Harmonic Motion as a projection of uniform circular motion.
3. What is meant by
angular harmonic oscillation?. Compute the time period of angular harmonic
oscillation.
4. Write down the
difference between simple harmonic motion and angular simple harmonic motion.
5. Discuss the simple
pendulum in detail.
6. Explain the
horizontal oscillations of a spring.
7. Describe the
vertical oscillations of a spring.
8. Write short notes on
the oscillations of liquid column in U-tube.
9. Discuss in detail
the energy in simple harmonic motion.
10. Explain in detail
the four different types of oscillations.
Numerical Problems
1. Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
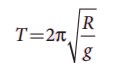
Solution
Earth is assumed to be a homogeneous sphere.
Its centre is at O and Radius = R
The hole is bored straight through the centre along its diameter. The acceleration due to gravity at the surface of the earth = g
Mass of the body dropped inside the hole = m
After time t, the depth it reached (inside the earth) = d
The value of ‘g’ decreases with deportation.
So acceleration due to gravity at deportation = ‘g'
i.e.,g' = g(l -d//R) = g( (R-d) / R) ...(1)
Let y be the distance from the centre of the earth
Then y = Radius - distance = R - d
Substitute y in (1)
g' = g y/R
Now, force on the body of mass m due to this new acceleration g' will be
F = mg' = mgy /R
and this force is directed towards the mean position O.
The body dropped in the hole will execute S.H.M Spring factor k = mg/Radius

2. Calculate the time period of the oscillation of a particle of mass m moving in the potential defined as

where E is the total energy of the particle.
Solution
Length of simple pendulum l = 0.9 m
Inclined plane with the horizontal plane α = 45°
Time period of oscillation of simple pendulum T = ?
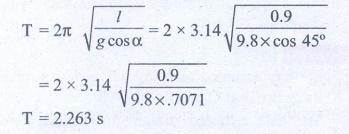
3. Consider a simple pendulum of length l = 0.9 m which is properly placed on a trolley rolling down on a inclined plane which is at θ = 45° with the horizontal. Assuming that the inclined plane is frictionless, calculate the time period of oscillation of the simple pendulum.
Answer: 0.86 s
4. A piece of wood of mass m is floating erect in a liquid whose density is ρ. If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is 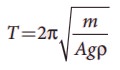
Solution:
Spring factor of liquid = Aρg
Inertra factor of wood piece = m
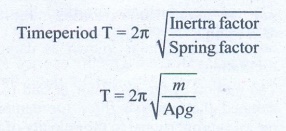
5. Consider two simple harmonic motion along x and y-axis having same frequencies but different amplitudes as x = A sin (ωt + φ) (along x axis) and y = B sin ωt (along y axis). Then show that
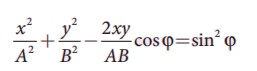
and also discuss the special cases when

Note: when a particle is subjected to two simple harmonic motion at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
Answer :
a. y=B/A x equation is a straight line passing through origin with positive slope.
b. y= - B/A x equation is a straight line passing through origin with negative slope.
c. 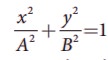 equation is an ellipse whose center is origin.
equation is an ellipse whose center is origin.
d. x2+y2 = A2, equation is a circle whose center is origin .
e. 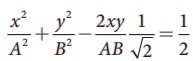 equation is an ellipse (oblique ellipse which means tilted ellipse)
equation is an ellipse (oblique ellipse which means tilted ellipse)
6. Show that for a particle executing simple harmonic motion
a. the average value of kinetic energy is equal to the average value of potential energy.
b. average potential energy = average kinetic energy = ½ (total energy)
Hint : average kinetic energy = <kinetic energy > = 1/T ∫0T(Kinetic energy) and average Potential energy = <Potential energy> =1/T ∫0T(Potential energy)
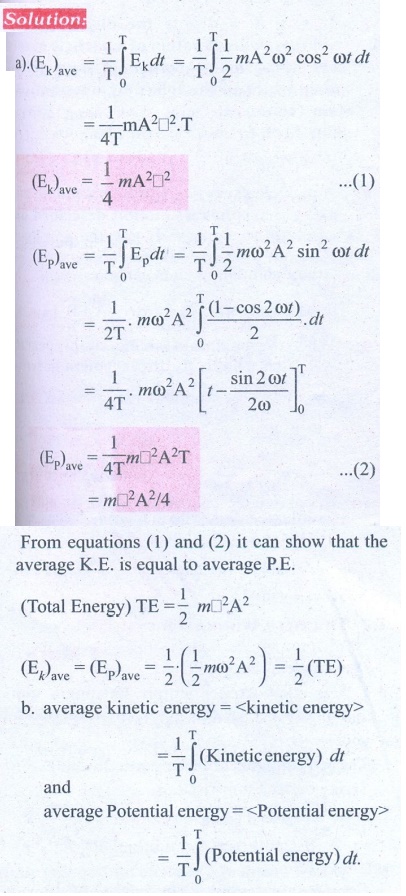
7. Compute the time period for the following system if the block of mass m is slightly displaced vertically down from its equilibrium position and then released. Assume that the pulley is light and smooth, strings and springs are light.
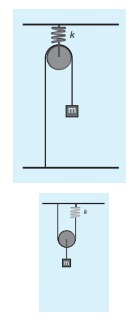
Hint and answer:
Case(a)
Pulley is fixed rigidly here. When the mass displace by y and the spring will also stretch by y. Therefore, F = T = ky
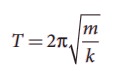
Case(b)
Mass displace by y, pulley also displaces by y. T = 4ky.
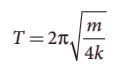
Related Topics