Oscillations | Physics - Solved Example Problems for Simple Harmonic Motion (SHM) | 11th Physics : UNIT 10 : Oscillations
Chapter: 11th Physics : UNIT 10 : Oscillations
Solved Example Problems for Simple Harmonic Motion (SHM)
Displacement, velocity, acceleration and its graphical representation – SHM
EXAMPLE 10.3
Which of the following represent simple harmonic motion?
(i) x = A sin ωt + B cos ωt
(ii) x = A sin ωt+ B cos 2ωt
(iii) x = A eiωt
(iv) x = A ln ωt
Solution
(i) x = A sin ωt + B cos ωt
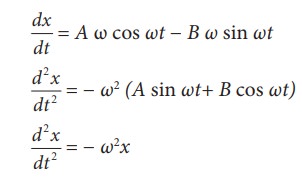
This differential equation is similar to the differential equation of SHM (equation 10.10).
Therefore, x = A sin ωt + B cos ωt represents SHM.
(ii) x =A sin ωt + B cos2ωt

This differential equation is not like the differential equation of a SHM (equation 10.10). Therefore, x = A sin ωt + B cos 2ωt does not represent SHM.
(iii) x=Aejωt
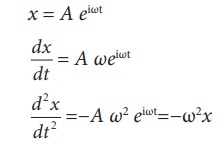
This differential equation is like the differential equation of SHM (equation 10.10). Therefore, x = A eiωt represents SHM.
(iv) x = A ln ωt
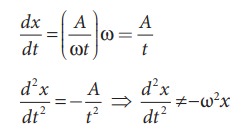
This differential equation is not like the differential equation of a SHM (equation 10.10). Therefore, x = A ln ωt does not represent SHM.
EXAMPLE 10.4
Consider a particle undergoing simple harmonic motion. The velocity of the particle at position x1 is v1 and velocity of the particle at position x2 is v2. Show that the ratio of time period and amplitude is
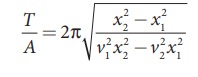
Solution
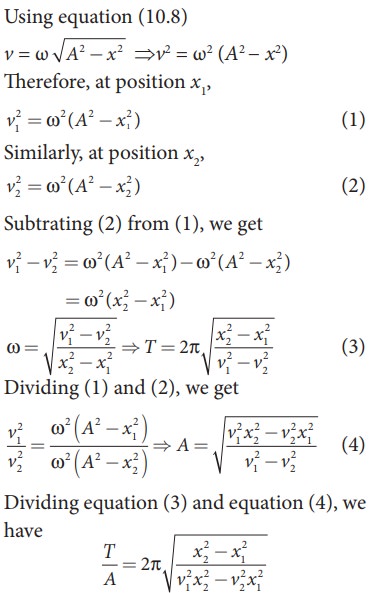
EXAMPLE 10.5
A nurse measured the average heart beats of a patient and reported to the doctor in terms of time period as 0.8s. Express the heart beat of the patient in terms of number of beats measured per minute.
Solution
Let the number of heart beats measured be f. Since the time period is inversely proportional to the heart beat, then
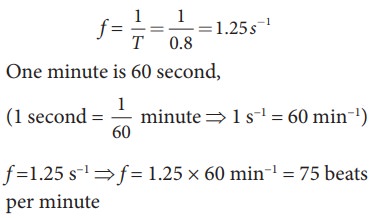
EXAMPLE 10.6
Calculate the amplitude, angular frequency, frequency, time period and initial phase for the simple harmonic oscillation given below
a. y = 0.3 sin (40πt + 1.1)
b. y = 2 cos (πt)
c. y = 3 sin (2πt − 1.5)
Solution
Simple harmonic oscillation equation is y = A sin(ωt + φ0) or y =A cos(ωt + φ0)

EXAMPLE 10.7
Show that for a simple harmonic motion, the phase difference between
a. displacement and velocity is π/2 radian or 90°.
b. velocity and acceleration is π/2 radian or 90°.
c. displacement and acceleration is π radian or 180°.
Solution
a. The displacement of the particle executing simple harmonic motion
y = A sinωt
Velocity of the particle is
v = Aωcos ωt = Aωsin(ωt+ π /2)
The phase difference between displacement and velocity is π/2.
b. The velocity of the particle is
v = A ω cos ωt
Acceleration of the particle is
a = Aω2sinωt = Aω2cos(ωt+ π /2)
The phase difference between velocity and acceleration is π/2.
c. The displacement of the particle is y = A sinωt
Acceleration of the particle is
a = − A ω2 sin ωt = A ω2 sin(ωt + π)
The phase difference between displacement and acceleration is π.
Related Topics