Chapter: 11th Physics : UNIT 10 : Oscillations
Simple Harmonic Motion (SHM)
SIMPLE
HARMONIC MOTION (SHM)
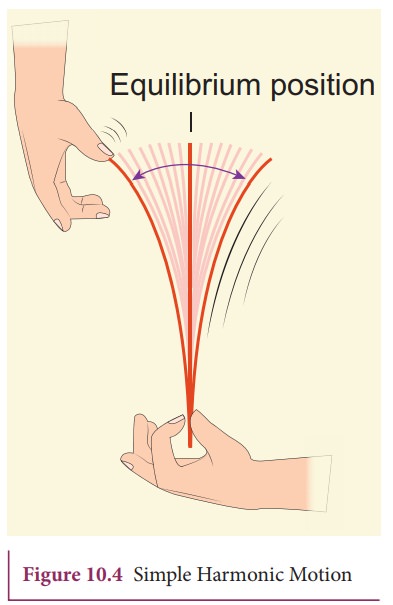
Simple
harmonic motion is a special type of oscillatory motion in which the
acceleration or force on the particle is directly proportional to its
displacement from a fixed point and is always directed towards that fixed
point. In one dimensional case, let x be
the displacement of the particle and ax
be the acceleration of the particle, then
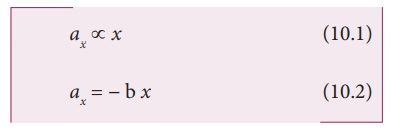
where
b is a constant which measures
acceleration per unit displacement and dimensionally it is equal to T−2. By multiplying by mass
of the particle on both sides of equation (10.2) and from Newton’s second law,
the force is

where k is a force constant which is defined as force per unit length. The negative sign indicates that displacement and force (or acceleration) are in opposite directions. This means that when the displacement of the particle is taken towards right of equilibrium position (x takes positive value), the force (or acceleration) will point towards equilibrium (towards left) and similarly, when the displacement of the particle is taken towards left of equilibrium position (x takes negative value), the force (or acceleration) will point towards equilibrium (towards right). This type of force is known as restoring force because it always directs the particle executing simple harmonic motion to restore to its original (equilibrium or mean) position. This force (restoring force) is central and attractive whose center of attraction is the equilibrium position.
In
order to represent in two or three dimensions, we can write using vector
notation

where ![]() is the displacement of the
particle from the chosen origin. Note that the force and displacement have a
linear relationship. This means that the exponent of force
is the displacement of the
particle from the chosen origin. Note that the force and displacement have a
linear relationship. This means that the exponent of force ![]() and the exponent of displacement
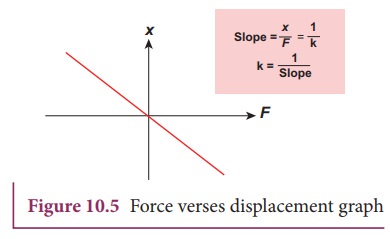
and the exponent of displacement ![]() are unity. The sketch between cause
(magnitude of force |
are unity. The sketch between cause
(magnitude of force | ![]() |) and
effect (magnitude of displacement |
|) and
effect (magnitude of displacement | ![]() |) is a straight line passing through second and fourth quadrant
as shown in Figure
10.5. By measuring slope 1/k , one
can find the numerical value of force constant k.
|) is a straight line passing through second and fourth quadrant
as shown in Figure
10.5. By measuring slope 1/k , one
can find the numerical value of force constant k.
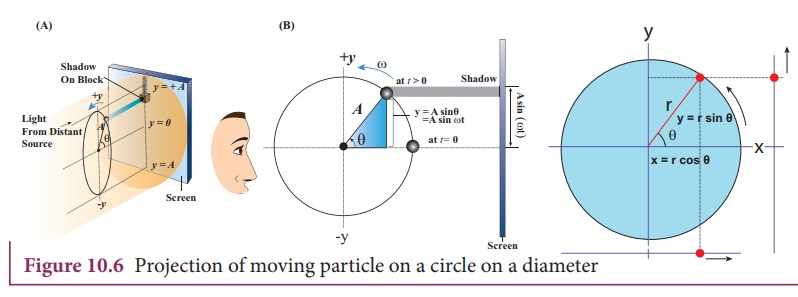
The projection of uniform circular motion on a diameter of SHM
Consider
a particle of mass m moving with
uniform speed v along the
circumference of a circle whose radius is r
in anti-clockwise direction (as shown in Figure 10.6). Let us assume that the
origin of the coordinate system coincides with the center O of the circle. If ω is the
angular velocity of the particle and θ
the angular displacement of the particle at any instant of time t, then θ = ωt. By projecting the
uniform circular motion on its diameter gives a simple harmonic motion.
This means that we can associate a
map (or a relationship) between uniform circular (or revolution) motion to
vibratory motion. Conversely, any vibratory motion or revolution can be mapped
to uniform circular motion. In other words, these two motions are similar in
nature.
Let
us first project the position of a particle moving on a circle, on to its
vertical diameter or on to a line parallel to vertical diameter as shown in
Figure 10.7. Similarly, we can do it for horizontal axis or a line parallel to
horizontal axis.
The following figures explain the position of particle at different time :
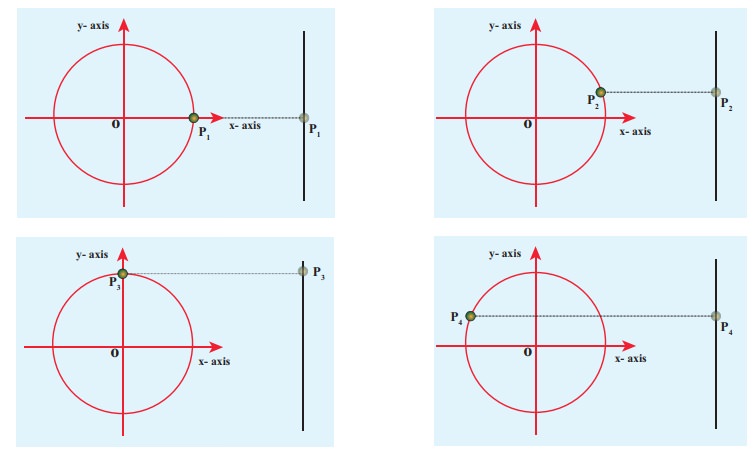
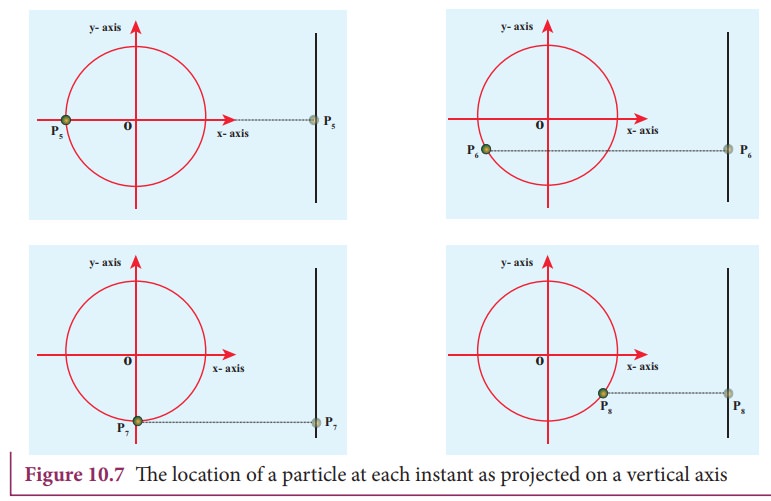
As
a specific example, consider a spring mass system (or oscillation of pendulum)
as shown in Figure 10.8. When the spring moves up and down (or pendulum moves
to and fro), the motion of the mass or bob is mapped to points on the circular
motion.
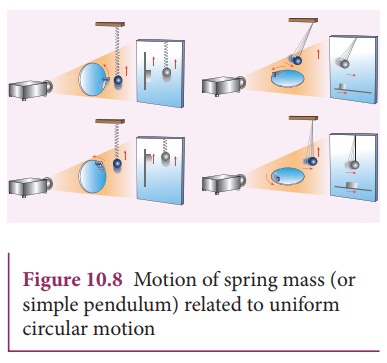
Thus, if a particle undergoes uniform circular motion then the projection of the particle on the diameter of the circle (or on a line parallel to the diameter ) traces straightline motion which is simple harmonic in nature. The circle is known as reference circle of the simple harmonic motion. The simple harmonic motion can also be defined as the motion of the projection of a particle on any diameter of a circle of reference.
Displacement, velocity, acceleration and its graphical representation – SHM
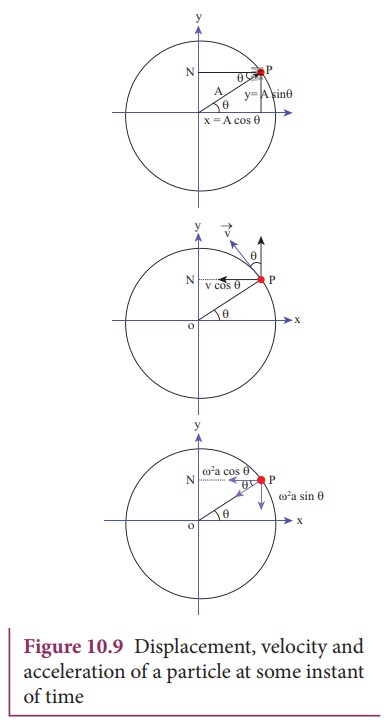
The distance travelled by the
vibrating particle at any instant of time t from its mean position is known as
displacement. Let P be the position of the particle on a circle of radius A at some instant
of time t as shown in Figure 10.9.
Then its displacement y at that instant of time t can be derived as follows In ∆OPN
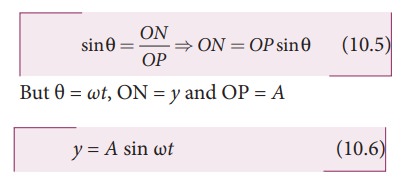
But
θ = ωt, ON = y and OP = A
The
displacement y takes maximum value
(which is equal to A) when sin ωt = 1. This maximum displacement from the mean position is known as amplitude (A)
of the vibrating particle. For simple harmonic motion, the amplitude is
constant. But, in general, for any motion other than simple harmonic, the
amplitude need not be constant, it may vary with time.
Velocity
The
rate of change of displacement is velocity. Taking derivative of equation
(10.6) with respect to time, we get

For
circular motion (of constant radius), amplitude A is a constant and further, for uniform circular motion, angular
velocity ω is a constant. Therefore,

From
equation (10.6),
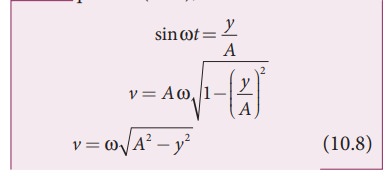
From
equation (10.8), when the displacement y =
0, the velocity v = ωA (maximum) and for the maximum displacement y
= A, the velocity v = 0 (minimum).
As
displacement increases from zero to maximum, the velocity decreases from
maximum to zero. This is repeated.
Since
velocity is a vector quantity, equation (10.7) can also be deduced by resolving
in to components.
Acceleration
The
rate of change of velocity is acceleration.
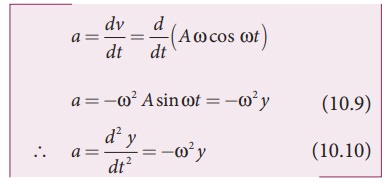
From
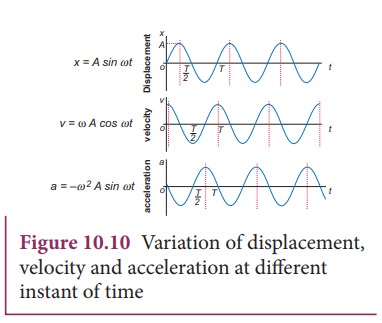
the Table 10.1 and figure 10.10, we observe that at the mean position

(y = 0), velocity of the particle is
maximum but the acceleration of the particle is zero. At the extreme position (y = ±A),
the velocity of the particle is zero but the acceleration is maximum ±Aω2 acting in the opposite
direction.
EXAMPLE 10.3
Which
of the following represent simple harmonic motion?
(i)
x = A sin ωt + B cos ωt
(ii)
x = A sin ωt+ B cos 2ωt
(iii)
x = A eiωt
(iv)
x = A ln ωt
Solution
(i) x = A sin ωt +
B cos ωt
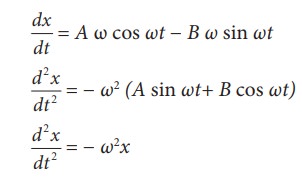
This
differential equation is similar to the differential equation of SHM (equation
10.10).
Therefore,
x = A sin ωt + B cos ωt represents SHM.
(ii) x =A sin ωt + B cos2ωt

This
differential equation is not like the differential equation of a SHM (equation
10.10). Therefore, x = A sin ωt + B cos 2ωt does not represent SHM.
(iii) x=Aejωt
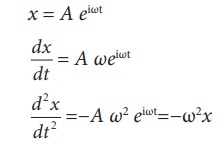
This
differential equation is like the differential equation of SHM (equation
10.10). Therefore, x = A eiωt represents SHM.
(iv) x = A ln ωt
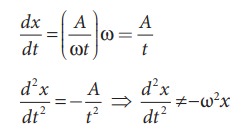
This
differential equation is not like the differential equation of a SHM (equation
10.10). Therefore, x = A ln ωt does not represent SHM.
EXAMPLE 10.4
Consider
a particle undergoing simple harmonic motion. The velocity of the particle at
position x1 is v1 and velocity of the
particle at position x2 is
v2. Show that the ratio of
time period and amplitude is
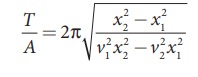
Solution
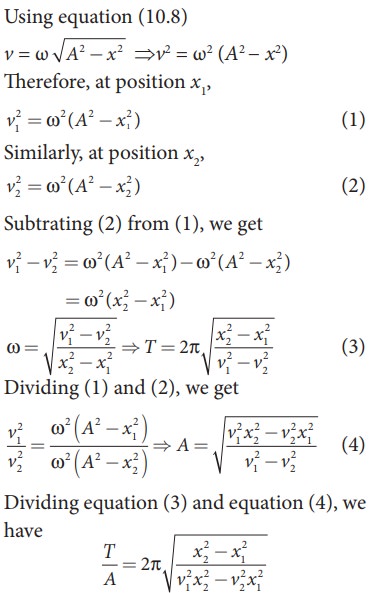
Time period, frequency, phase, phase difference and epoch in SHM.
(i) Time period
The
time period is defined as the time taken by a particle to complete one
oscillation. It is usually denoted by T. For one complete revolution, the time
taken is t = T, therefore
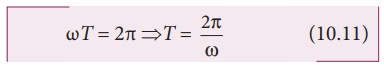
Then,
the displacement of a particle executing simple harmonic motion can be written
either as sine function or cosine function.

where
T represents the time period. Suppose the time t is replaced by t + T, then the
function
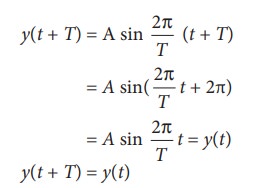
Thus,
the function repeats after one time period.
This
y(t) is an example of periodic function.
(ii) Frequency and angular frequency
The
number of oscillations produced by the particle per second is called frequency.
It is denoted by f. SI unit for
frequency is s−1 or hertz (In symbol, Hz).
Mathematically,
frequency is related to time period by

The number
of cycles (or revolutions) per second is called angular frequency. It is
usually denoted by the Greek small letter ‘omega’, ω. Comparing equation
(10.11) and equation (10.12), angular frequency and frequency are related
by

SI unit for
angular frequency is rad s−1. (read it as radian per second)
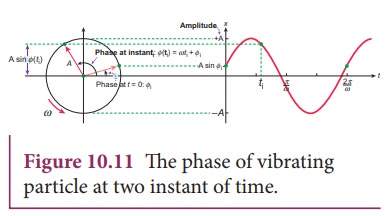
(iii) Phase
The phase of a vibrating particle at any
instant completely specifies the state of the particle.
It expresses the position and direction of
motion of the particle at that instant with respect to its mean position
(Figure 10.11).
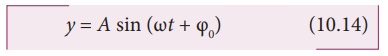
where ωt
+ φ0 = φ is called the phase of the vibrating particle. At time t =
0s (initial time), the phase φ = φ0 is called epoch (initial phase)
where φ0 is called the angle of epoch. Phase
difference: Consider two
particles executing simple harmonic motions. Their equations
are y1 = A sin(ωt + φ1) and y2 =
A sin(ωt + φ 2), then the phase difference ∆φ= (ωt + φ2)
− (ωt + φ1) = φ2
−φ1.
EXAMPLE 10.5
A nurse measured the average heart beats of a patient
and reported to the doctor in terms of time period as 0.8s. Express the heart beat of the patient in terms of number of
beats measured per minute.
Solution
Let the number of heart beats measured be f. Since the time period is inversely
proportional to the heart beat, then
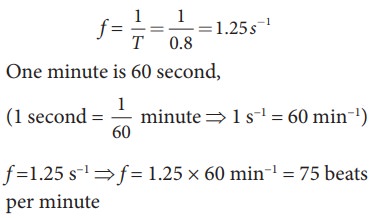
EXAMPLE 10.6
Calculate
the amplitude, angular frequency, frequency, time period and initial phase for
the simple harmonic oscillation given below
a. y = 0.3 sin (40πt + 1.1)
b.
y = 2 cos (πt)
c.
y = 3 sin (2πt − 1.5)
Solution
Simple
harmonic oscillation equation is y = A sin(ωt + φ0) or y =A cos(ωt +
φ0)

EXAMPLE 10.7
Show that for a simple harmonic motion, the phase difference between
a. displacement and velocity is π/2 radian or 90°.
b. velocity and acceleration is π/2 radian or 90°.
c.
displacement and acceleration is π radian or 180°.
Solution
a. The displacement of the particle executing
simple harmonic motion
y = A sinωt
Velocity
of the particle is
v = Aωcos ωt = Aωsin(ωt+ π /2)
The
phase difference between displacement and velocity is π/2.
b.
The velocity of the particle is
v
= A ω cos ωt
Acceleration
of the particle is
a = Aω2sinωt
= Aω2cos(ωt+ π /2)
The
phase difference between velocity and acceleration is π/2.
c.
The displacement of the particle is y = A sinωt
Acceleration
of the particle is
a = − A ω2 sin ωt = A ω2 sin(ωt + π)
The
phase difference between displacement and acceleration is π.
Related Topics