Chapter: 11th Physics : UNIT 10 : Oscillations
The projection of uniform circular motion on a diameter of SHM
The projection of uniform circular motion on a diameter of SHM
Consider a particle of mass m moving with uniform speed v along the circumference of a circle whose radius is r in anti-clockwise direction (as shown in Figure 10.6). Let us assume that the origin of the coordinate system coincides with the center O of the circle. If ω is the angular velocity of the particle and θ the angular displacement of the particle at any instant of time t, then θ = ωt. By projecting the uniform circular motion on its diameter gives a simple harmonic motion.
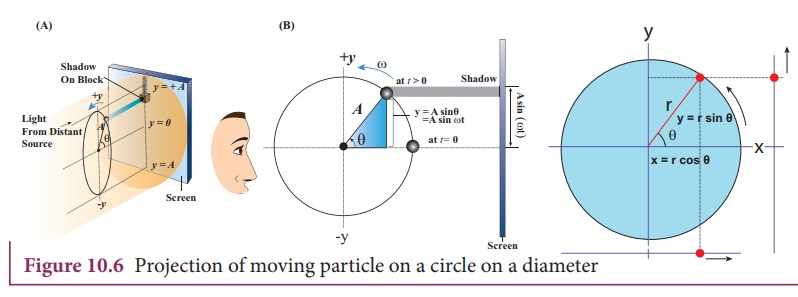
This means that we can associate a map (or a relationship) between uniform circular (or revolution) motion to vibratory motion. Conversely, any vibratory motion or revolution can be mapped to uniform circular motion. In other words, these two motions are similar in nature.
Let us first project the position of a particle moving on a circle, on to its vertical diameter or on to a line parallel to vertical diameter as shown in Figure 10.7. Similarly, we can do it for horizontal axis or a line parallel to horizontal axis.
The following figures explain the position of particle at different time :
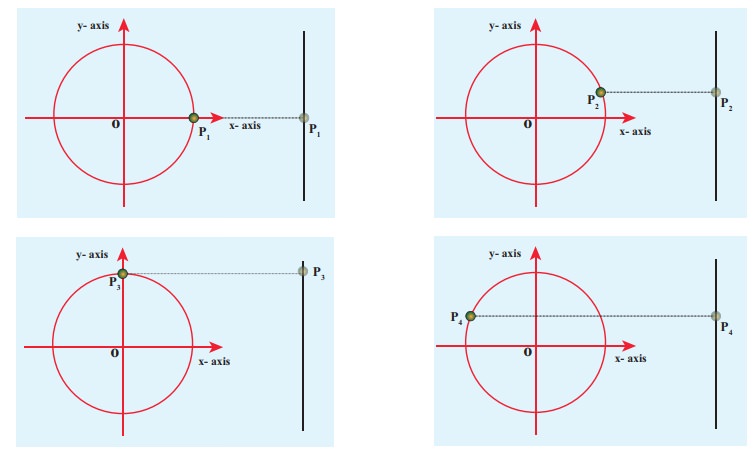
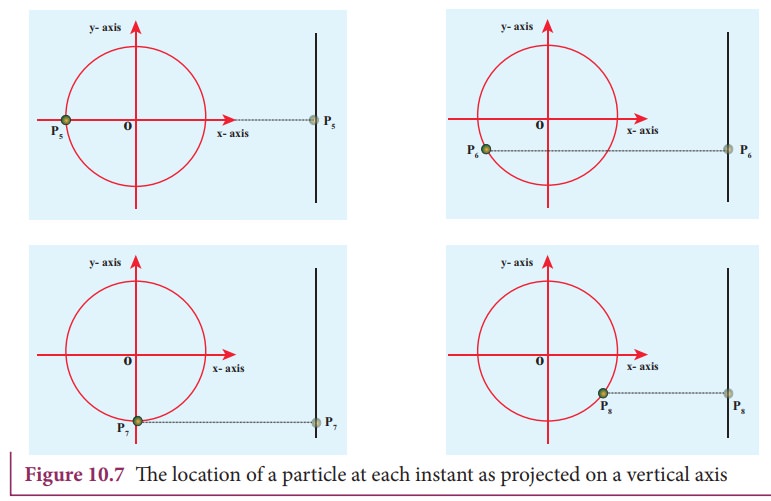
As a specific example, consider a spring mass system (or oscillation of pendulum) as shown in Figure 10.8. When the spring moves up and down (or pendulum moves to and fro), the motion of the mass or bob is mapped to points on the circular motion.
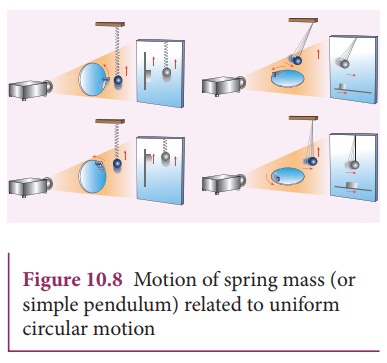
Thus, if a particle undergoes uniform circular motion then the projection of the particle on the diameter of the circle (or on a line parallel to the diameter ) traces straightline motion which is simple harmonic in nature. The circle is known as reference circle of the simple harmonic motion. The simple harmonic motion can also be defined as the motion of the projection of a particle on any diameter of a circle of reference.
Related Topics