Long Questions and Answer

Oscillations (Physics)

Long Answers Questions

1. What is meant by simple harmonic oscillation?. Give examples and explain why every simple harmonic motion is a periodic motion whereas the converse need not be true.

Simple harmonic motion:

● The acceleration or force on the particle is directly proportional to its displacement from a fixed point and is always directed towards that fixed point.

● In one dimensional case, let x be the displacement of the particle and a_x be the acceleration of the particle,

● a_x ∝ x : a_x = − b x where b is a constant which measures acceleration per unit displacement and dimensionally it is equal to T⁻².

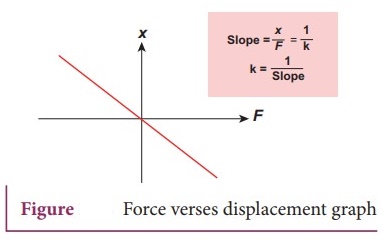
● By multiplying by mass of the particle on both sides of equation and from Newtons second law, the force is F_x = − kx where k is a force constant which is defined as force per unit length.

● The negative sign indicates that displacement and force (or acceleration) are in opposite directions.

● When the displacement of the particle is taken towards right of equilibrium position (x takes positive value), the force (or acceleration) will point towards equilibrium (towards left) and similarly, when the displacement of the particle is taken towards left of equilibrium position (x takes negative value), the force (or acceleration) will point towards equilibrium (towards right).

● This type of force is known as restoring force because it always directs the particle executing simple harmonic motion to restore to its original (equilibrium or mean) position.

● This force (restoring force) is central and attractive whose center of attraction is the equilibrium position.

● In vector notation  = − k, where  is the displacement of the particle from the chosen origin.

● The exponent of force  and the exponent of displacement  are unity.

2. Describe Simple Harmonic Motion as a projection of uniform circular motion.

● Consider a particle of mass m moving with uniform speed v along the circumference of a circle whose radius is r in anti-clockwise direction .

● If ω is the angular velocity of the particle and θ the angular displacement of the particle at any instant of time t, then θ = ωt.

● Consider a spring mass system (or oscillation of pendulum). When the spring moves up and down (or pendulum moves to and fro), the motion of the mass or bob is mapped to points on the circular motion.

● If a particle undergoes uniform circular motion then the projection of the particle on the diameter of the circle (or on a line parallel to the diameter) traces straight line motion which is simple harmonic in nature.

● The circle is known as reference circle of the simple harmonic motion. The simple harmonic motion can also be defined as the motion of the projection of a particle on any diameter of a circle of reference.

3. What is meant by angular harmonic oscillation?. Compute the time period of angular harmonic oscillation.

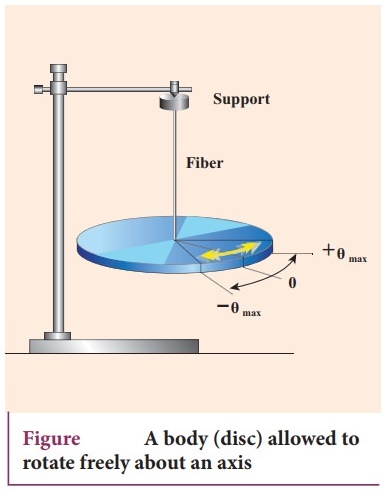
● When a body is allowed to rotate freely about oscillation is known as the angular oscillation. The point at which the resultant torque acting on the body is taken to be zero is called mean position.

● If the body is displaced from the mean position, then the resultant torque acts such that it is proportional to the angular displacement and this torque has a tendency to bring the body towards the mean position.

● Let be the angular displacement of the body and the resultant torque , acting on the body is 

● k is the restoring torsion constant, which is torque per unit angular displacement. If I is the moment of inertia of the body and  is the angular acceleration then

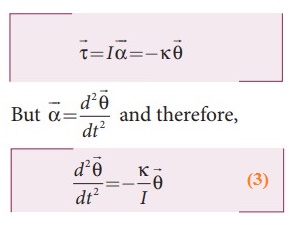
● This differential equation resembles simple harmonic differential equation. So, comparing equation with simple harmonic motion given in equation.

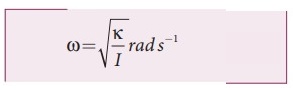………….. (4)

The frequency of the angular harmonic motion is 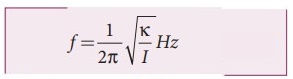 ………………(5)

and the time period of the oscillation is .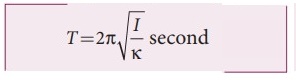

4. Write down the difference between simple harmonic motion and angular simple harmonic motion.

5. Discuss the simple pendulum in detail.

● A pendulum is a mechanical system which exhibits periodic motion. It has a bob with mass m suspended by a long string (assumed to be mass less and inextensible string) and the other end is fixed on a stand.

● When a pendulum is displaced through a small displacement from its equilibrium position and released, the bob of the pendulum executes to and fro motion.

● Let l be the length of the pendulum which is the distance between the point of suspension and the centre of gravity of the bob.

● Two forces act on the bob of the pendulum at any displaced position, (i) The gravitational force acting on the body 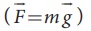 which acts vertically downwards, (ii) The tension in the string  which acts along the string to the point of suspension.

● Resolving the gravitational force into its components:

(a) Normal component: The component along the string but in opposition to the direction of tension. F_as = mg cosθ.

(b) Tangential component:

The component perpendicular to the string i.e, along tangential direction of arc of swing.

F_ps = mg sinθ.

● The normal component of the force is,

T- F_as = m (v²/l)

v- Speed of bob

T - mg cosθ = m (v²/l)           ……….(1)

● The tangential force is nothing but the restoring force.

Applying newton's second law,

m ( d²s / dt² ) + F_ps = 0 ;

m ( d²s / dt² ) = − F_ps

m ( d²s / dt² ) = − mg sinθ             ……………(2)

● Arc length, s = lθ            ………… (3)

∴ d²s / dt² = l ( d²θ / dt² )             ……………. (4)

 Substitute (4) in (2) we get

6. Explain the horizontal oscillations of a spring.

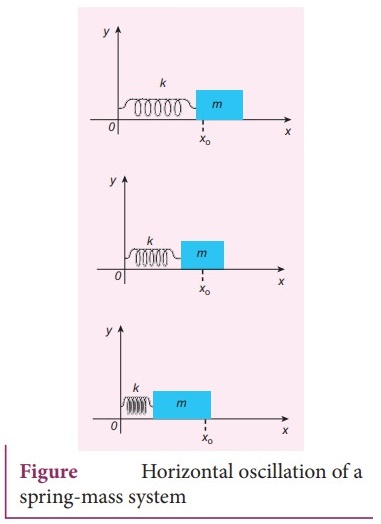
Horizontal oscillation of a spring-mass system

● Consider a system containing a block of mass m attached to a mass less spring with stiffness constant or force constant or spring constant k placed on a smooth horizontal surface (frictionless surface)

● Let X₀ be the equilibrium position or mean position of mass m when it is left undisturbed.

● Suppose the mass is displaced through a small displacement x towards right from its equilibrium position and then released, it will oscillate back and forth about its mean position X₀. 

● Let F be the restoring force (due to stretching of the spring) which is proportional to the amount of displacement of block. For one dimensional motion. F ∝ x; F = − k x

● Negative sign implies that the restoring force will always act opposite to the direction of the Y displacement. The restoring force is linear with the displacement.

● If we apply a very large stretching force, then the amplitude of oscillations becomes very large. The oscillation of the system is not linear and hence, it is called non-linear oscillation.

● From Newton's second law. executing simple harmonic motion, is given by for the particle.

m [ d²x / dt² ] = − kx ;

d²x / dt² = − [k/m] x              ……….(1)

● Comparing equation (1) with simple harmonic motion equation.

we get ω² = k / m

● Which means the angular frequency or natural frequency of the oscillator is

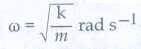 ……… (2)

● Natural frequency of the oscillator is

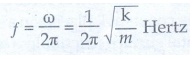 ………. (3)

● Time period of the oscillation is

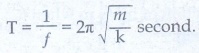 ………..(4)

● In simple harmonic motion, the time period of oscillation is independent of amplitude. This is valid only if the amplitude of oscillation is small.

7. Describe the vertical oscillations of a spring.

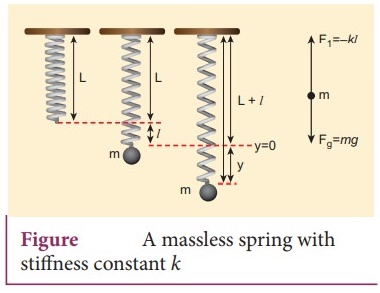
A massless spring with stiffness constant k

● Consider a mass-less spring with stiffness constant or force constant k attached to a ceiling. Let the length of the spring before loading mass m be L. If the block of mass m is attached to the other end of spring, then the spring elongates by a length l

● Let F1 be the restoring force due to stretching of spring. Due to mass m, the gravitational force acts vertically downward. When the system is under equilibrium. F₁ + mg = 0  …………. 1

● But the spring elongates by small displacement I₁ therefore,

F₁ ∝ l ⇒ F₁ = − kl         ………. (2)

Substituting equation (2) in equation (1). we get − kl + mg = 0

mg = kl or m / k = l / g          ……………… 3

● Suppose we apply a very small external force on the mass such that the mass further displaces downward by a displacement y. then it will oscillate up and down. The restoring force due to this stretching of spring (total extension of spring is (y + l) is F₂ ∝ (y + l)

F₂ = − k(y + l) = − ky – kl       ….. (4)

By drawing the free body diagram for this case, we get

− ky − kl + mg = m (d²y / dt² )      …………..(5)

The net force acting on the mass due to this stretching is F = F₂ + mg

F = − ky − kl + mg       ……….. (6)

● The gravitational force opposes the restoring force. Substituting equation (3) in equation (6), we get

F = − ky − kl + kl = − ky

Applying Newton's law, we get

m [d²y / dt² ] = −ky

d²y / dt² = [k / m] y         ………….(7)

● The above equation is in the form of simple harmonic differential equation.

The time period as 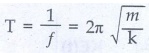 second

● The time period can be rewritten using equation (3)

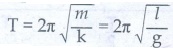
The acceleration due to gravity g can be computed from the formula g = 4π²(l/ T²)ms^-2

8. Write short notes on the oscillations of liquid column in U-tube.

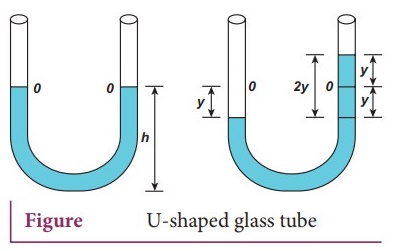
U-shaped glass tube

● Consider a U-shaped glass tube which consists of two open arms with uniform cross-sectional area A.

● Let us pour a non-viscous uniform incompressible liquid of density ρ in the U-shaped tube to a height h

● If the liquid and tube are not disturbed then the liquid surface will be in equilibrium position O.

● It means the pressure as measured at any point on the liquid is the same and also at the surface on the arm (edge of the tube on either side), which balances with the atmospheric pressure.

● Due to this the level of liquid in each arm will be the same. By blowing air one can provide sufficient force in one arm, and the liquid gets disturbed from equilibrium position O, which means, the pressure at blown arm is higher than the other arm.

● This creates difference in pressure which will cause the liquid to oscillate for a very short duration of time about the mean or equilibrium position and finally comes to rest.

● Time period of the oscillation is

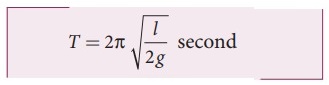
9. Discuss in detail the energy in simple harmonic motion.

a. Expression for Potential Energy

● For the simple harmonic motion, the force and the displacement are related by Hooke's law 

● Since force is a vector quantity in three dimensions, it has three components. Further, the force in the above equation is a conservative force field; such a force can be derived from a scalar function which has only one component.

● In one dimensional case F = − kx           ………… (1).

● The work done by the conservative force field is independent of path.

● The potential energy U can be calculated from the following expression.

F = − dU / dx     …………(2)

Comparing (1) and (2). we get

− dU/dx = − kx ; dU = kxdx

● This work done by the force F during a small displacement dx stores as potential energy

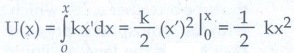 ………. (3)

From equation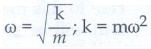 

Substitute the value of force constant k = mω² in equation (3).

We get U(x) = 1/2 mω²x²

● Where ω is the natural frequency of the oscillating system. For the particle executing simple harmonic motion from equation x = A sin ωt. we get

U(t) = 1/2 mω²A²Sin²ωt      ………… (4)

b. Expression for Kinetic Energy

Kinetic energy KE = 1/2 mv_x² = 1/2 m(dx/dt)²

Since the particle is executing simple harmonic motion,

x = A sin ωt Therefore.

Velocity is v_x. = dx / dt = A ω cos(ωt)

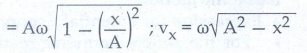
Hence. KE = 1/2 mv_x² = 1/2 mω² (A² – x² )      …….(6)

KE = 1/2 mω²A²cos²ωt      ………. (7)

c. Expression for Total Energy

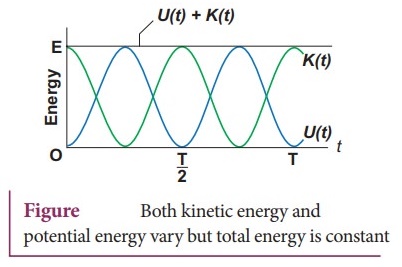
Total energy is the sum of kinetic energy and potential energy E = KE + U  …….. (8);

E = 1/2 mω² (A² – x² ) + 1/2 mω²x²

Hence cancelling x² term.

E = 1/2 m ω² A² = Constant ………… (9)

From equation (4) and equation (7).

We get the total energy as

E = [ 1/2 m ω² A² Sin²ωt ] + [ 1/2 m ω² A² cos²ωt ]

E = 1/2 m ω² A² ( Sin²ωt + cos²ωt)

From trigonometry identity. (Sin²ωt + cos²ωt) = 1

E = 1/2 m ω² A² = Constant.

This gives the law of conservation of total energy. Thus the amplitude of simple harmonic oscillator can be expressed in terms of total energy.

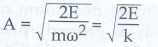
10. Explain in detail the four different types of oscillations.

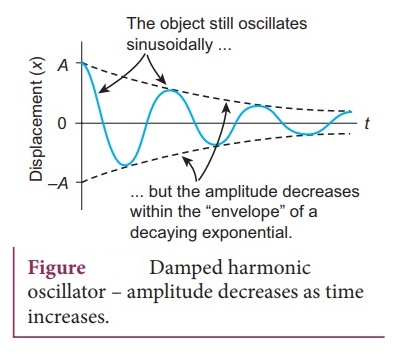
Damped oscillations:

● During the oscillation of a simple pendulum, the amplitude of the oscillation is constant and also the total energy of the oscillator is constant. In a medium, due to the presence of friction and air drag, the amplitude of oscillation decreases as time progresses.

● The oscillation is not sustained and the energy of the SHM decreases gradually indicating the loss of energy. The energy lost is absorbed by the surrounding medium. This type of oscillatory motion is known as damped oscillation.

● If an oscillator moves in a resistive medium, its amplitude goes on decreasing and the energy of the oscillator is used to do work against the resistive medium.

● The motion of the oscillator is said to be damped and in this case, the resistive force (or damping force) is proportional to the velocity of the oscillator.

● Examples: (i) The oscillations of a pendulum (including air friction) or pendulum oscillating inside an oil filled container, (ii) Electromagnetic oscillations in a tank circuit, (iii) Oscillations in a dead beat and ballistic galvanometers.

Maintained oscillations:

● While playing in swing, the oscillations will stop after a few cycles, this is due to damping. To avoid damping we have to supply a push to sustain oscillations.

● By supplying energy from an external source, the amplitude of the oscillation can be made constant. Such vibrations are known as maintained vibrations.

● Example: The vibration of a tuning fork getting energy from a battery or from external power supply.

Forced oscillations:

● Any oscillator driven by an external periodic agency to overcome the damping is known as forced oscillator or driven oscillator.

● In this type of vibration, the body executing vibration initially vibrates with its natural frequency and due to the presence of external periodic force, the body later vibrates with the frequency of the applied periodic force. Such vibrations are known as forced vibrations.

● Example: Sound boards of stringed instruments.

Resonance:

● The frequency of external periodic force (or driving force) matches with the natural frequency of the vibrating body (driven).

● As a result the oscillating body begins to vibrate such that its amplitude increases at each step and ultimately it has a large amplitude. Such a phenomenon is known as resonance and the corresponding vibrations are known as resonance vibrations.

● Example: The breaking of glass due to sound.