Energy in Simple Harmonic Motion

ENERGY IN SIMPLE HARMONIC MOTION

a. Expression for Potential Energy

For the simple harmonic motion, the force and the displacement are related by Hooke’s law

Since force is a vector quantity, in three dimensions it has three components. Further, the force in the above equation is a conservative force field; such a force can be derived from a scalar function which has only one component. In one dimensional case

As we have discussed in unit 4 of volume I, the work done by the conservative force field is independent of path. The potential energy U can be calculated from the following expression.

Comparing (10.63) and (10.64), we get

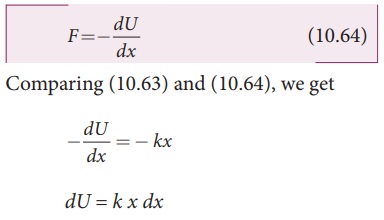
This work done by the force F during a small displacement dx stores as potential energy

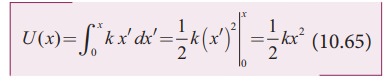
From equation (10.22), we can substitute the value of force constant k = m ω2 in equation (10.65),

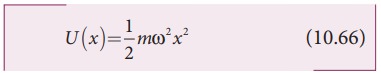
where ω is the natural frequency of the oscillating system. For the particle executing simple harmonic motion from equation (10.6), we get

x = A sin ωt

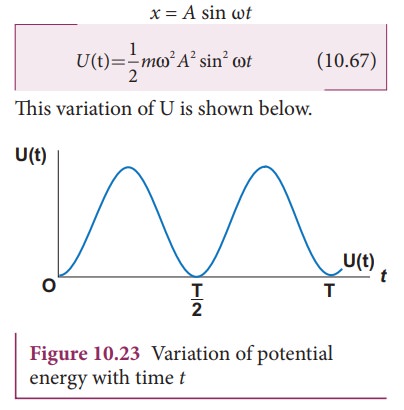
b. Expression for Kinetic Energy

Kinetic energy

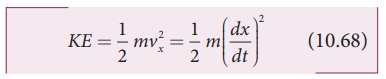
Since the particle is executing simple harmonic motion, from equation (10.6)

x = A sin ωt

Therefore, velocity is

This variation with time is shown below.

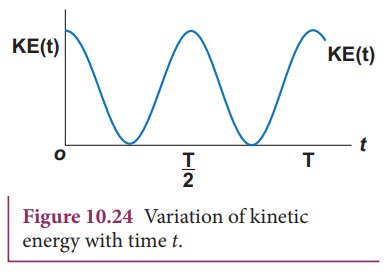
c. Expression for Total Energy

Total energy is the sum of kinetic energy and potential energy

Alternatively, from equation (10.67) and equation (10.72), we get the total energy as

E =1/2 mω ² A ² sin ² ωt + 1/2 mω ² A² cos² ωt

= 1/2 mω ² A² (sin² ω t +cos² ωt)

From trigonometry identity,

(sin²Ï‰t + cos²Ï‰t) = 1

E = 1/2 mω² A² = constant

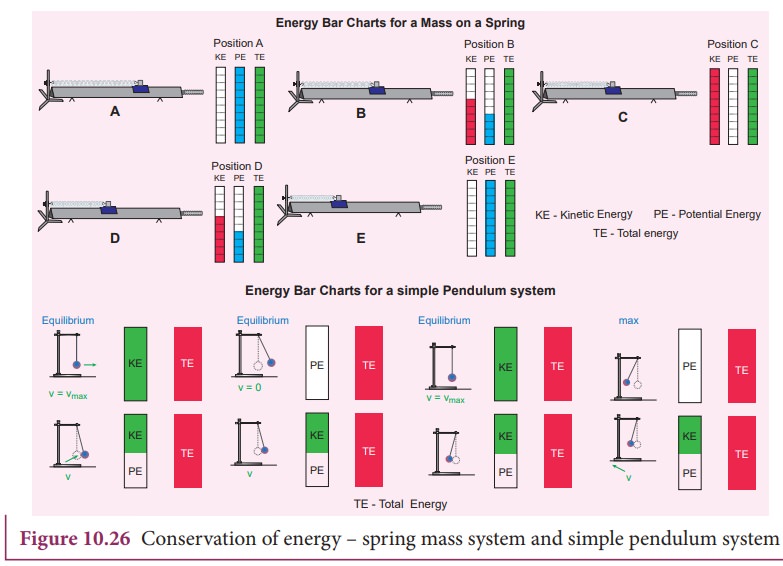
which gives the law of conservation of total energy. This is depicted in Figure 10.26

Thus the amplitude of simple harmonic oscillator, can be expressed in terms of total energy.

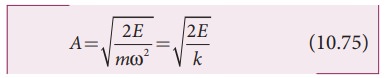
EXAMPLE 10.15

Write down the kinetic energy and total energy expressions in terms of linear momentum, For one-dimensional case.

Solution

Kinetic energy is KE= 1/2 mv_x²

Multiply numerator and denominator by m

KE= [1/2m] m² v_x² = [1/2m] (mv_x )² = [1/2m] p_x²

where, p_x is the linear momentum of the particle executing simple harmonic motion.

Total energy can be written as sum of kinetic energy and potential energy, therefore, from equation (10.73) and also from equation (10.75), we get

E= KE +U( x) = [1/2m] p_x² + 1/2 mω² x² = constant

EXAMPLE 10.16

Compute the position of an oscillating particle when its kinetic energy and potential energy are equal.

Solution

Since the kinetic energy and potential energy of the oscillating particle are equal,

1/2 mω ² (A² − x ² ) = 1/2 mω² x²

A² − x² = x²

2x² = A²

x = ±A/√2