Vertical oscillations of a spring - Linear Simple Harmonic Oscillator (LHO)

Vertical oscillations of a spring

Let us consider a massless spring with stiffness constant or force constant k attached to a ceiling as shown in Figure 10.15. Let the length of the spring before loading mass m be L. If the block of mass m is attached to the other end of spring, then the spring elongates by a length l. Let F1 be the restoring force due to stretching of spring. Due to mass m, the gravitational force acts vertically downward. We can draw free-body diagram for this system as shown in Figure 10.15. When the system is under equilibrium,

But the spring elongates by small displacement l, therefore,

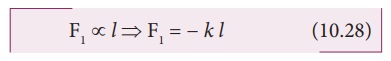
Substituting equation (10.28) in equation (10.27), we get

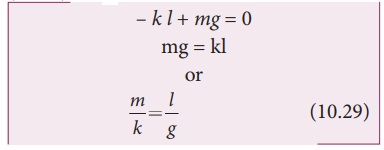
Suppose we apply a very small external force on the mass such that the mass further displaces downward by a displacement y, then it will oscillate up and down. Now, the restoring force due to this stretching of spring (total extension of spring is y + l ) is

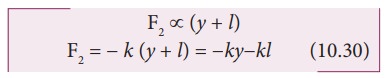
Since, the mass moves up and down with acceleration d2y/dt2, by drawing the free body, diagram for this case, we get

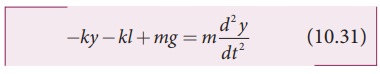
The net force acting on the mass due to this stretching is

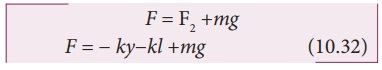
The gravitational force opposes the restoring force. Substituting equation (10.29) in equation (10.32), we get

F = −ky âˆ’ kl + kl = −ky

Applying Newton’s law, we get

The above equation is in the form of simple harmonic differential equation. Therefore, we get the time period as

The time period can be rewritten using equation (10.29)

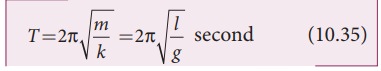
The acceleration due to gravity g can be computed from the formula

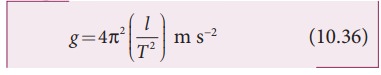
EXAMPLE 10.8

A spring balance has a scale which ranges from 0 to 25 kg and the length of the scale is 0.25m. It is taken to an unknown planet X where the acceleration due to gravity is 11.5 m s−1. Suppose a body of mass M kg is suspended in this spring and made to oscillate with a period of 0.50 s. Compute the gravitational force acting on the body.

Solution

Let us first calculate the stiffness constant of the spring balance by using equation (10.29),

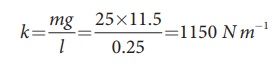
The time period of oscillations is given by T=2π√M/√k, , where M is the mass of the body.

Since, M is unknown, rearranging, we get

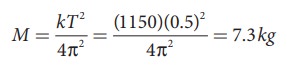
The gravitational force acting on the body is W = Mg = 7.3 × 11.5 = 83.95 N ≈ 84 N