Chapter: 11th Physics : UNIT 10 : Oscillations
Combinations of springs - Linear Simple Harmonic Oscillator (LHO)
Combinations of springs

Spring constant or force constant, also called as stiffness constant, is a measure of the stiffness of the spring. Larger the value of the spring constant, stiffer is the spring. This implies that we need to apply more force to compress or elongate the spring. Similarly, smaller the value of spring constant, the spring can be stretched (elongated) or compressed with lesser force. Springs can be connected in two ways. Either the springs can be connected end to end, also known as series connection, or alternatively, connected in parallel. In the following subsection, we compute the effective spring constant when
a. Springs are connected in series
b. Springs are connected in parallel
a. Springs connected in series
When two or more springs are connected in series, we can replace (by removing) all the springs in series with an equivalent spring (effective spring) whose net effect is the same as if all the springs are in series connection. Given the value of individual spring constants k1, k2, k3,... (known quantity), we can establish a mathematical relationship to find out an effective (or equivalent) spring constant ks (unknown quantity). For simplicity, let us consider only two springs whose spring constant are k1 and k2 and which can be attached to a mass m as shown in Figure 10.17. The results thus obtained can be generalized for any number of springs in series.
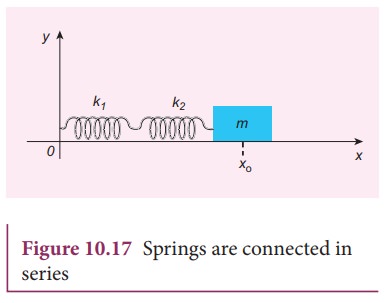
Let F be the applied force towards right as shown in Figure 10.18. Since the spring constants for different spring are different and the connection points between them is not rigidly fixed, the strings can stretch in different lengths. Let x1 and x2 be the elongation of springs from their equilibrium position (un-stretched position) due to the applied force F. Then, the net displacement of the mass point is

From Hooke’s law, the net force
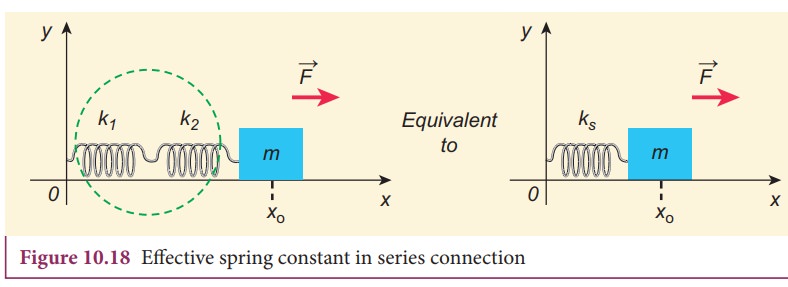
For springs in series connection
−k1x1 = −k2x2 = F
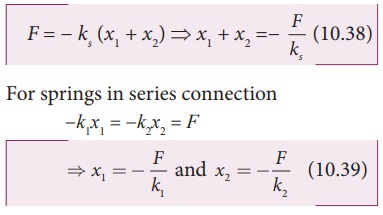
Therefore, substituting equation (10.39) in equation (10.38), the effective spring constant can be calculated as
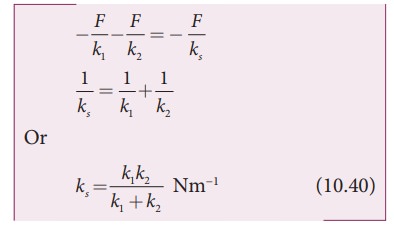
Suppose we have n springs connected in series, the effective spring constant in series is
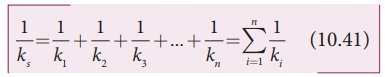
If all spring constants are identical i.e., k1 = k2 =... = kn = k then
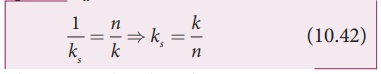
This means that the effective spring constant reduces by the factor n. Hence, for springs in series connection, the effective spring constant is lesser than the individual spring constants.
From equation (10.39), we have,
k1x1 = k2x2
Then the ratio of compressed distance or elongated distance x1 and x2 is

The elastic potential energy stored in first and second springs are V1=1/2 k1x12 and V2=1/2 k2x22 respectively. Then, their ratio is
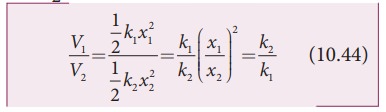
EXAMPLE 10.9
Consider two springs whose force constants are 1 N m−1 and 2 N m−1 which are connected in series. Calculate the effective spring constant (ks ) and comment on ks .
Solution
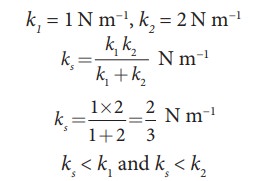
ks < k1 and ks < k
Therefore, the effective spring constant is lesser than both k1 and k2.
b. Springs connected in parallel
When two or more springs are connected in parallel, we can replace (by removing) all these springs with an equivalent spring (effective spring) whose net effect is same as if all the springs are in parallel connection. Given the values of individual spring constants to be k1,k2,k3, ... (known quantities), we can establish a mathematical relationship to find out an effective (or equivalent) spring constant kp (unknown quantity). For simplicity, let us consider only two springs of spring constants k1and k2 attached to a mass m as shown in Figure 10.19. The results can be generalized to any number of springs in parallel.
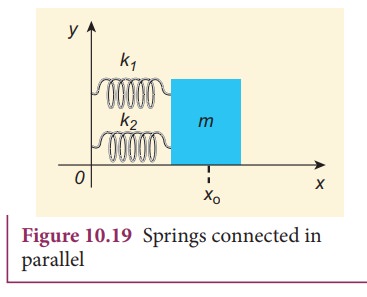
Let the force F be applied towards right as shown in Figure 10.20. In this case, both the springs elongate or compress by the same amount of displacement. Therefore, net force for the displacement of mass m is

where kp is called effective spring constant. Let the first spring be elongated by a displacement x due to force F1 and second spring be elongated by the same displacement x due to force F2, then the net force
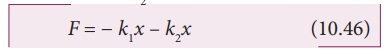
Equating equations (10.46) and (10.45), we get

Generalizing, for n springs connected in parallel,

If all spring constants are identical i.e., k1 = k2= ... = kn = k then

This implies that the effective spring constant increases by a factor n. Hence, for the springs in parallel connection, the effective spring constant is greater than individual spring constant.
EXAMPLE 10.10
Consider two springs with force constants 1 N m−1 and 2 N m−1 connected in parallel. Calculate the effective spring constant (kp ) and comment on kp.
Solution
k1 = 1 N m−1, k2 = 2 N m−1
kp = k1 + k2 N m−1
kp = 1 + 2 = 3 N m−1
kp > k1 and kp > k2
Therefore, the effective spring constant is greater than both k1 and k2.
EXAMPLE 10.11
Calculate the equivalent spring constant for the following systems and also compute if all the spring constants are equal:
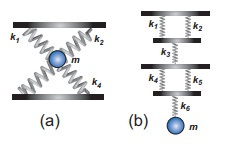
Solution
a. Since k1 and k2 are parallel, ku = k1 + k2 Similarly, k3 and k4 are parallel, therefore, kd = k3 + k4
But ku and kd are in series,
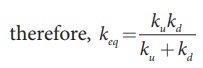
If all the spring constants are equal then, k1 = k2 = k3 = k4 = k
Which means, ku = 2k and kd = 2k
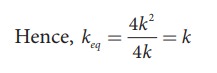
b. Since k1 and k2 are parallel, kA = k1 + k2 Similarly, k4 and k5 are parallel, therefore, kB = k4 + k5
But kA, k3, kB, and k6 are in series,
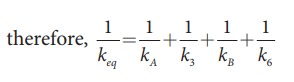
If all the spring constants are equal then, k1 = k2 = k3 = k4 = k5 = k6 = k which means, kA = 2k and kB = 2k
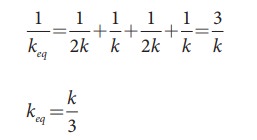
keq = k/3
EXAMPLE 10.12
A mass m moves with a speed v on a horizontal smooth surface and collides with a nearly massless spring whose spring constant is k. If the mass stops after collision, compute the maximum compression of the spring.
Solution
When the mass collides with the spring, from the law of conservation of energy “the loss in kinetic energy of mass is gain in elastic potential energy by spring”.
Let x be the distance of compression of spring, then the law of conservation of energy
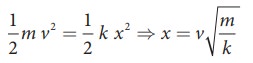
Related Topics