Chapter: 11th Physics : UNIT 10 : Oscillations
Multiple Choice Questions - Physics: Oscillations
Oscillations (Physics)
Multiple Choice Questions
1. In a simple harmonic oscillation, the acceleration against displacement for one complete oscillation will be
a) an ellipse
b) a circle
c) a parabola
d) a straight line
Answer: d) a straight line
2. A particle executing SHM crosses points A and B with the same velocity. Having taken 3 s in passing from A to B, it returns to B after another 3 s. The time period is
a) 15 s
b) 6 s
c) 12 s
d) 9 s
Answer: c) 12 s
Solution:
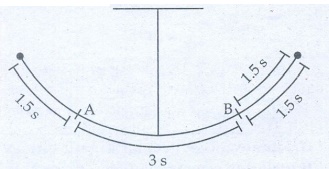
Total time taken to complete one oscilation is = 2 (1.5 + 3 + 1.5) s
= 2 (6) s
= 12 s
3. The length of a second’s pendulum on the surface of the Earth is 0.9 m. The length of the same pendulum on surface of planet X such that the acceleration of the planet X is n times greater than the Earth is
(a) 0.9n
(b) 0.9/n m
(c) 0.9n2m
(d) 0.9/n2
Answer: a) 0.9n
Solution:
T = 2π √(1 /g) ; L ∝ g
Lx ∝ gx ; LE ∝gE
Lx / LE = ngE / gE
Lx = LE n
Lx = 0.9 n
4. A simple pendulum is suspended from the roof of a school bus which moves in a horizontal direction with an acceleration a, then the time period is
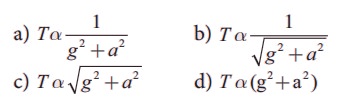
Answer: b) 1 / √ [g2 + a2]
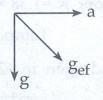
T ∝ 1 / √ [g2 + a2]
gef2 = a2 + g2;
gef = √[a2 + g2]
5. Two bodies A and B whose masses are in the ratio 1:2 are suspended from two separate massless springs of force constants kA and kB respectively. If the two bodies oscillate vertically such that their maximum velocities are in the ratio 1:2, the ratio of the amplitude A to that of B is
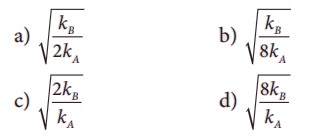
Answer: b) √[kB / 8kA]
Solution:
A = √[2E / K]. E = 1/2 mv2
AA / AB = √[ (mAvA) / kA ] × [ KB / (mBvB2 )]
AA / AB = {√[mv2 ] / kA } × { KB / 2m(4v2) }
AA / AB = KB / gkA
6. A spring is connected to a mass m suspended from it and its time period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillation is
a) T’=√2T
b) T’=T/√2
c) T’=√2√T
d) T’=√2/√T
Answer: b) T’ = T/√2
Solution:
T = 2π √(l / g)
T´ = 2π√( 1/2 × l/g )
T´ = T / √2
7. The time period for small vertical oscillations of block of mass m when the masses of the pulleys are negligible and spring constant k1 and k2 is
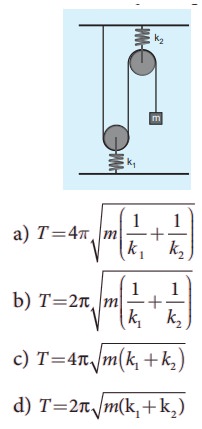
Answer: a) T = 4π√[m (1/k1 + 1/k2 )]
8. A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according as y = k t2, where y is vertical distance covered and k = 1 ms−2, its time period becomes T2. Then T12/T22 is (g=10ms-2)
(a) 5/6
(b) 11/10
(c) 6/5
(d) 5/6
Answer: c) 6 / 5
Solution:
a = d2y / dt2 = 2k = 2(1) = 2ms-2
T1 = 2π√(l/g) = 2π√(l /10)
T2 = 2π√[l / (g+a)] = 2π√(l /12)
T12 / T22 = 12/ 10 = 6 / 5
9. An ideal spring of spring constant k, is suspended from the ceiling of a room and a block of mass M is fastened to its lower end. If the block is released when the spring is un-stretched, then the maximum extension in the spring is
(a) 4 Mg/k
(b) Mg/k
(c) 2 Mg/k
(d) Mg/2k
Answer: c) 2(Mg/k)
Solution:
Mgx = (1/2) kx2
Mg = (½) (kx)
x = 2(Mg/k)
10. A pendulum is hung in a very high building oscillates to and fro motion freely like a simple harmonic oscillator. If the acceleration of the bob is 16 ms−2 at a distance of 4 m from the mean position, then the time period is
a) 2 s
b) 1 s
c) 2πs
(d) πs
Answer: d) π s
Solution:
a = −ω2y
ω = √[a / y] = √[16/4]
ω = 2 rad s −1
T = 2π / w = 2π / 2 = π s
11. A hollow sphere is filled with water. It is hung by a long thread. As the water flows out of a hole at the bottom, the period of oscillation will
a) first increase and then decrease
b) first decrease and then increase
c) increase continuously
d) decrease continuously
Answer: a) first increase and then decrease
Solution:
T = 2π / ω ;
ω = √(K/M)
T = 2π / √(K/M) = 2π √(M/K) ;
T ∝√M
12. The damping force on an oscillator is directly proportional to the velocity. The units of the constant of proportionality are
a) kg m s−1
b) kg m s−2
c) kg s−1
d) kg s
Answer: c) kg s-1
F∝ v
F = Kv
K = F/V ;
K = kgms-1 / ms-1
K = kg s-1
13. When a damped harmonic oscillator completes 100 oscillations, its amplitude is reduced to 1/3 of its initial value. What will be its amplitude when it completes 200 oscillations?.
a) 1/5
b) 2/3
c) 1/6
d) 1/9
Answer: d) 1 / 9
14. Which of the following differential equations represents a damped harmonic oscillator ?

Answer: b) d2y/dt2 + γ dy/dt + y = 0
15. If the inertial mass and gravitational mass of the simple pendulum of length l are not equal, then the time period of the simple pendulum is

Answer: a) T = 2π √[ mil / mgg ]
T = 2π √(l / k) ;
l = m ;
m/k= l / g ;
k = mg / l
T = 2π √[mi / (mgg / l )];
T = 2π √[mil / mgg]
Answers:
1) d 2) c 3) a 4) b
5) b 6) b 7) a 8) c
9) c 10) d 11) a 12) c
13) d 14) b 15) a
Related Topics