Short Questions and Answer

Oscillations (Physics)

Short Answers Questions

1. What is meant by periodic and non- periodic motion?. Give any two examples, for each motion.

● Periodic motion: Any motion which repeats itself in a fixed time interval is known as periodic motion. Examples: Hands in pendulum clock, swing of a cradle, the revolution of the Earth around the Sun, waxing and waning of Moon, etc.

● Non-Periodic motion: Any motion which does not repeat itself after a regular interval of time non-periodic motion. Example: Occurrence of Earth quake, eruption of volcano, etc.

2. What is meant by force constant of a spring?

Force constant is defined as-force

Eg.: Per unit displacement.

Force constant = Force / Displacement

Example:

● Oscillations of a loaded spring

● Vibrations of a turning force

3. Define time period of simple harmonic motion.

The time period is defined as the time taken by a particle to complete one oscillation. It is usually denoted by T. For one complete revolution, the time taken is t = T.

therefore, ωT = 2π / T

=> T = 2π / ω

4. Define frequency of simple harmonic motion.

● The number of oscillations produced by the particle per second is called frequency. It is denoted by f. SI unit for frequency is S⁻¹ or hertz (In symbol. Hz).

● Angular frequency is related to time period by ω = 2π / T

● The number of cycles (or revolutions) per second is called angular frequency.

● It is usually denoted by the Greek small letter ‘omega'. ω.

● Angular frequency and frequency are related by ω = 2π f

● SI unit for angular frequency is rad S⁻¹.

5. What is an epoch?.

The displacement time t = 0 s (initial time), the phase ϕ = ϕ_o is called epoch, (initial phase) where ϕ_o is called the angle of epoch.

6. Write short notes on two springs connected in series.

● Consider only two springs whose spring constant are k₁ and k₂ and which can be attached to a mass m.

● The results thus obtained can be generalized for any number of springs in series.

● For springs in series connection, reciprocal of effective spring is equal to reciprocal of individual spring.

7. Write short notes on two springs connected in parallel.

● Consider only two springs of spring constants k₁ and k₂ attached to a mass m.

● The results can be generalized to any number of springs in parallel.

● For springs in parallel, the effective spring constant is equal to sun of individual spring constant.

8. Write down the time period of simple pendulum.

● The angular frequency of the oscillator is

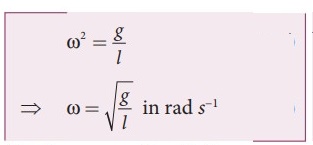
● The frequency of oscillations is 

, 

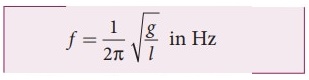and time period of oscillations is 

.

9. State the laws of simple pendulum?.

● Law of length: For a given value of acceleration due to gravity, the time period of a simple pendulum is directly proportional to the square root of length of the pendulum. T ∝ √l

● Law of acceleration: For a fixed length, the time period of a simple pendulum is inversely proportional to square root of acceleration due to gravity. T ∝ 1/√g

10. Write down the equation of time period for linear harmonic oscillator.

● From Newton's second law, we can write the equation for the particle executing simple harmonic motion

m = d²x / dt² = kx ;

d²x / dt² = − (k/m) x

● Comparing the equation with simple harmonic motion equation, we get,

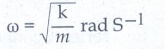
● Natural frequency of the oscillator is 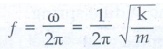 Hertz and the time period of the oscillation is 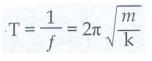 second.

11. What is meant by free oscillation?.

● When the oscillator is allowed to oscillate by displacing its position from equilibrium position.

● It oscillates with a frequency which is equal to the natural frequency of the oscillator.

12. Explain damped oscillation. Give an example.

● Due to the presence of friction and air drag, the amplitude of oscillation decreases as time progresses.

● It implies that the oscillation is not sustained and the energy of the SHM decreases gradually indicating the loss of energy.

● The energy lost is absorbed by the surrounding medium. This type of oscillatory motion is known as damped oscillation.

● Examples: (i) The oscillations of a pendulum (including air friction) or pendulum oscillating inside an oil filled container, (ii) Electromagnetic oscillations in a tank circuit, (iii) Oscillations in a dead beat and ballistic galvanometers.

13. Define forced oscillation. Give an example.

● The body executing vibration initially vibrates with its natural frequency and due to the presence of external periodic force, the body later vibrates with the frequency of the applied periodic force.

● Such vibrations are known as forced vibrations.

● Example: Sound boards of stringed instruments.

14. What is meant by maintained oscillation?. Give an example.

Give an example.

● While playing in swing, the oscillations will stop after a few cycles, this is due to damping. To avoid damping we have to supply a push to sustain oscillations. By supplying energy from an external source, the amplitude of the oscillation can be made constant. Such vibrations are known as maintained vibrations.

● Example: The vibration of a tuning fork getting energy from a battery or from external power supply.

15. Explain resonance. Give an example.

● The frequency of external periodic force (or driving force) matches with the natural frequency of the vibrating body (driven). As a result the oscillating body begins to vibrate such that its amplitude increases at each step and ultimately it has a large amplitude. Such a phenomenon is known as resonance and the corresponding vibrations are known as resonance vibrations.

● Example: The breaking of glass due to sound.