Book Back Numerical Problems

Oscillations (Physics)

Numerical Problems

1. Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is

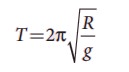
Solution

Earth is assumed to be a homogeneous sphere.

Its centre is at O and Radius = R

The hole is bored straight through the centre along its diameter. The acceleration due to gravity at the surface of the earth = g

Mass of the body dropped inside the hole = m

After time t, the depth it reached (inside the earth) = d

The value of ‘g’ decreases with deportation.

So acceleration due to gravity at deportation = ‘g'

i.e.,g' = g(l -d//R) = g( (R-d) / R) ...(1)

Let y be the distance from the centre of the earth

Then y = Radius - distance = R - d

Substitute y in (1)

g' = g y/R

Now, force on the body of mass m due to this new acceleration g' will be

F = mg' = mgy /R

and this force is directed towards the mean position O.

The body dropped in the hole will execute S.H.M Spring factor k = mg/Radius

2. Calculate the time period of the oscillation of a particle of mass m moving in the potential defined as

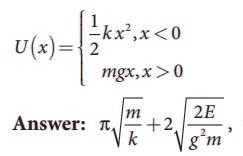
where E is the total energy of the particle.

Solution

Length of simple pendulum l = 0.9 m

Inclined plane with the horizontal plane α = 45°

Time period of oscillation of simple pendulum T = ?

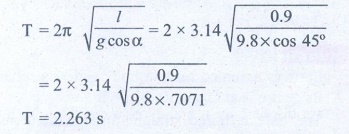
3. Consider a simple pendulum of length l = 0.9 m which is properly placed on a trolley rolling down on a inclined plane which is at θ = 45° with the horizontal. Assuming that the inclined plane is frictionless, calculate the time period of oscillation of the simple pendulum.

Answer: 0.86 s

4. A piece of wood of mass m is floating erect in a liquid whose density is ρ. If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is 

Solution:

Spring factor of liquid = Aρg

Inertra factor of wood piece = m

5. Consider two simple harmonic motion along x and y-axis having same frequencies but different amplitudes as x = A sin (ωt + φ) (along x axis) and y = B sin ωt (along y axis). Then show that

and also discuss the special cases when

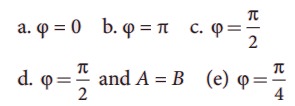
Note: when a particle is subjected to two simple harmonic motion at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.

Answer :

a. y=B/A x equation  is  a  straight  line passing through origin with positive slope.

b.  y= - B/A x equation is a straight line passing through origin with negative slope.

c. 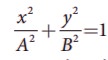 equation is an ellipse whose center is origin.

d. x2+y2 = A2, equation is a circle whose center is origin .

e. 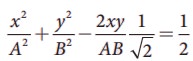 equation is an ellipse (oblique ellipse which means tilted ellipse)

6. Show that for a particle executing simple harmonic motion

a. the average value of kinetic energy is equal to the average value of potential energy.

b. average potential energy = average kinetic energy = ½ (total energy)

Hint : average kinetic energy = <kinetic energy > = 1/T ∫0T(Kinetic energy) and average Potential energy = <Potential energy> =1/T ∫0T(Potential energy)

7. Compute the time period for the following system if the block of mass m is slightly displaced vertically down from its equilibrium position and then released. Assume that the pulley is light and smooth, strings and springs are light.

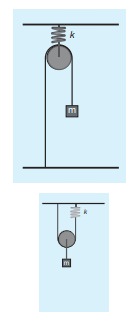
Hint and answer:

Case(a)

Pulley is fixed rigidly here. When the mass displace by y and the spring will also stretch by y. Therefore, F = T = ky

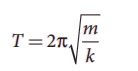
Case(b)

Mass displace by y, pulley also displaces by y. T = 4ky.