Chapter: 11th Physics : UNIT 10 : Oscillations
Solved Example Problems for Physics: Oscillations
Numerical Problems
1. Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
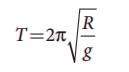
Solution
Earth is assumed to be a homogeneous sphere.
Its centre is at O and Radius = R
The hole is bored straight through the centre along its diameter. The acceleration due to gravity at the surface of the earth = g
Mass of the body dropped inside the hole = m
After time t, the depth it reached (inside the earth) = d
The value of ‘g’ decreases with deportation.
So acceleration due to gravity at deportation = ‘g'
i.e.,g' = g(l -d//R) = g( (R-d) / R) ...(1)
Let y be the distance from the centre of the earth
Then y = Radius - distance = R - d
Substitute y in (1)
g' = g y/R
Now, force on the body of mass m due to this new acceleration g' will be
F = mg' = mgy /R
and this force is directed towards the mean position O.
The body dropped in the hole will execute S.H.M Spring factor k = mg/Radius
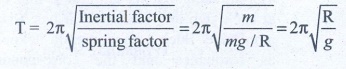
2. Calculate the time period of the oscillation of a particle of mass m moving in the potential defined as
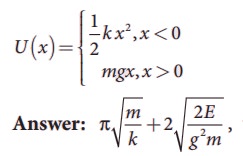
where E is the total energy of the particle.
Solution
Length of simple pendulum l = 0.9 m
Inclined plane with the horizontal plane α = 45°
Time period of oscillation of simple pendulum T = ?
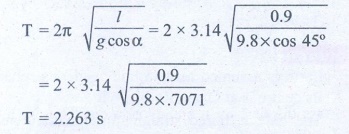
3. Consider a simple pendulum of length l = 0.9 m which is properly placed on a trolley rolling down on a inclined plane which is at θ = 45° with the horizontal. Assuming that the inclined plane is frictionless, calculate the time period of oscillation of the simple pendulum.
Answer: 0.86 s
4. A piece of wood of mass m is floating erect in a liquid whose density is ρ. If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is 
Solution:
Spring factor of liquid = Aρg
Inertra factor of wood piece = m
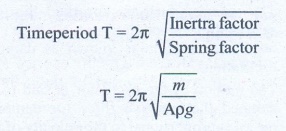
5. Consider two simple harmonic motion along x and y-axis having same frequencies but different amplitudes as x = A sin (ωt + φ) (along x axis) and y = B sin ωt (along y axis). Then show that
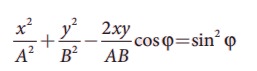
and also discuss the special cases when

Note: when a particle is subjected to two simple harmonic motion at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
Answer :
a. y=B/A x equation is a straight line passing through origin with positive slope.
b. y= - B/A x equation is a straight line passing through origin with negative slope.
c. 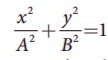 equation is an ellipse whose center is origin.
equation is an ellipse whose center is origin.
d. x2+y2 = A2, equation is a circle whose center is origin .
e. 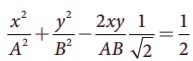 equation is an ellipse (oblique ellipse which means tilted ellipse)
equation is an ellipse (oblique ellipse which means tilted ellipse)
6. Show that for a particle executing simple harmonic motion
a. the average value of kinetic energy is equal to the average value of potential energy.
b. average potential energy = average kinetic energy = ½ (total energy)
Hint : average kinetic energy = <kinetic energy > = 1/T ∫0T(Kinetic energy) and average Potential energy = <Potential energy> =1/T ∫0T(Potential energy)
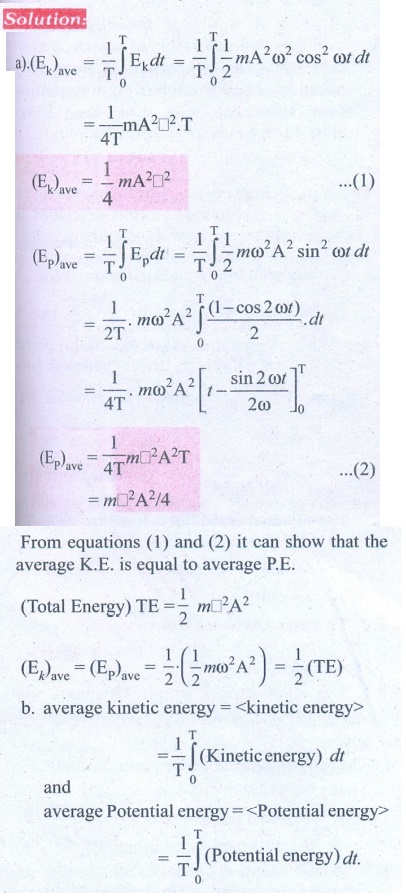
7. Compute the time period for the following system if the block of mass m is slightly displaced vertically down from its equilibrium position and then released. Assume that the pulley is light and smooth, strings and springs are light.
Hint and answer:
Case(a)
Pulley is fixed rigidly here. When the mass displace by y and the spring will also stretch by y. Therefore, F = T = ky
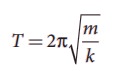
Case(b)
Mass displace by y, pulley also displaces by y. T = 4ky.
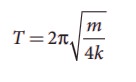
Displacement, velocity, acceleration and its graphical representation – SHM
EXAMPLE 10.3
Which of the following represent simple harmonic motion?
(i) x = A sin ωt + B cos ωt
(ii) x = A sin ωt+ B cos 2ωt
(iii) x = A eiωt
(iv) x = A ln ωt
Solution
(i) x = A sin ωt + B cos ωt
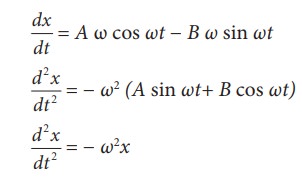
This differential equation is similar to the differential equation of SHM (equation 10.10).
Therefore, x = A sin ωt + B cos ωt represents SHM.
(ii) x =A sin ωt + B cos2ωt

This differential equation is not like the differential equation of a SHM (equation 10.10). Therefore, x = A sin ωt + B cos 2ωt does not represent SHM.
(iii) x=Aejωt
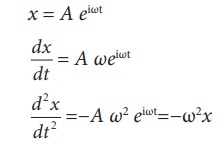
This differential equation is like the differential equation of SHM (equation 10.10). Therefore, x = A eiωt represents SHM.
(iv) x = A ln ωt
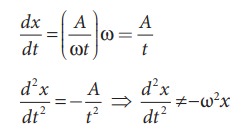
This differential equation is not like the differential equation of a SHM (equation 10.10). Therefore, x = A ln ωt does not represent SHM.
EXAMPLE 10.4
Consider a particle undergoing simple harmonic motion. The velocity of the particle at position x1 is v1 and velocity of the particle at position x2 is v2. Show that the ratio of time period and amplitude is
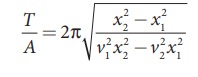
Solution
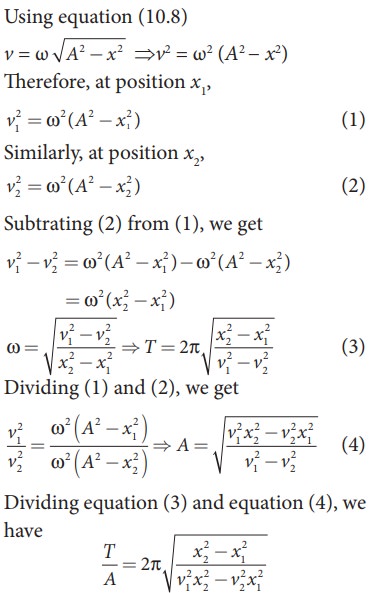
EXAMPLE 10.5
A nurse measured the average heart beats of a patient and reported to the doctor in terms of time period as 0.8s. Express the heart beat of the patient in terms of number of beats measured per minute.
Solution
Let the number of heart beats measured be f. Since the time period is inversely proportional to the heart beat, then
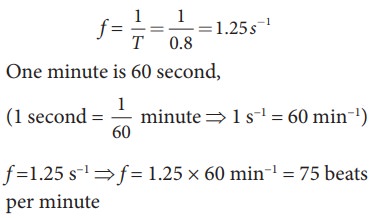
EXAMPLE 10.6
Calculate the amplitude, angular frequency, frequency, time period and initial phase for the simple harmonic oscillation given below
a. y = 0.3 sin (40πt + 1.1)
b. y = 2 cos (πt)
c. y = 3 sin (2πt − 1.5)
Solution
Simple harmonic oscillation equation is y = A sin(ωt + φ0) or y =A cos(ωt + φ0)

EXAMPLE 10.7
Show that for a simple harmonic motion, the phase difference between
a. displacement and velocity is π/2 radian or 90°.
b. velocity and acceleration is π/2 radian or 90°.
c. displacement and acceleration is π radian or 180°.
Solution
a. The displacement of the particle executing simple harmonic motion
y = A sinωt
Velocity of the particle is
v = Aωcos ωt = Aωsin(ωt+ π /2)
The phase difference between displacement and velocity is π/2.
b. The velocity of the particle is
v = A ω cos ωt
Acceleration of the particle is
a = Aω2sinωt = Aω2cos(ωt+ π /2)
The phase difference between velocity and acceleration is π/2.
c. The displacement of the particle is y = A sinωt
Acceleration of the particle is
a = − A ω2 sin ωt = A ω2 sin(ωt + π)
The phase difference between displacement and acceleration is π.
Solved Example Problems for Linear Simple Harmonic Oscillator (LHO)
Vertical oscillations of a spring
EXAMPLE 10.8
A spring balance has a scale which ranges from 0 to 25 kg and the length of the scale is 0.25m. It is taken to an unknown planet X where the acceleration due to gravity is 11.5 m s−1. Suppose a body of mass M kg is suspended in this spring and made to oscillate with a period of 0.50 s. Compute the gravitational force acting on the body.
Solution
Let us first calculate the stiffness constant of the spring balance by using equation (10.29),
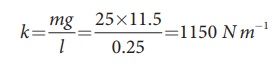
The time period of oscillations is given by T=2π√M/√k, , where M is the mass of the body.
Since, M is unknown, rearranging, we get
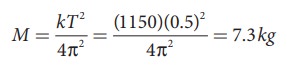
The gravitational force acting on the body is W = Mg = 7.3 × 11.5 = 83.95 N ≈ 84 N
Combinations of springs
EXAMPLE 10.9
Consider two springs whose force constants are 1 N m−1 and 2 N m−1 which are connected in series. Calculate the effective spring constant (ks ) and comment on ks .
Solution
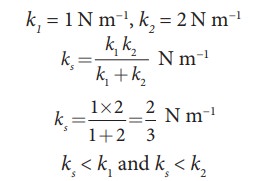
ks < k1 and ks < k
Therefore, the effective spring constant is lesser than both k1 and k2.
EXAMPLE 10.10
Consider two springs with force constants 1 N m−1 and 2 N m−1 connected in parallel. Calculate the effective spring constant (kp ) and comment on kp.
Solution
k1 = 1 N m−1, k2 = 2 N m−1
kp = k1 + k2 N m−1
kp = 1 + 2 = 3 N m−1
kp > k1 and kp > k2
Therefore, the effective spring constant is greater than both k1 and k2.
EXAMPLE 10.11
Calculate the equivalent spring constant for the following systems and also compute if all the spring constants are equal:
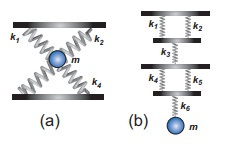
Solution
a. Since k1 and k2 are parallel, ku = k1 + k2 Similarly, k3 and k4 are parallel, therefore, kd = k3 + k4
But ku and kd are in series,
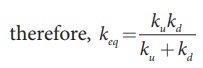
If all the spring constants are equal then, k1 = k2 = k3 = k4 = k
Which means, ku = 2k and kd = 2k
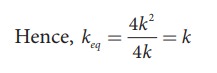
b. Since k1 and k2 are parallel, kA = k1 + k2 Similarly, k4 and k5 are parallel, therefore, kB = k4 + k5
But kA, k3, kB, and k6 are in series,
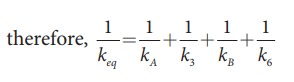
If all the spring constants are equal then, k1 = k2 = k3 = k4 = k5 = k6 = k which means, kA = 2k and kB = 2k
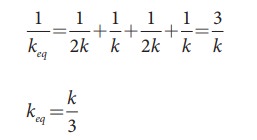
keq = k/3
EXAMPLE 10.12
A mass m moves with a speed v on a horizontal smooth surface and collides with a nearly massless spring whose spring constant is k. If the mass stops after collision, compute the maximum compression of the spring.
Solution
When the mass collides with the spring, from the law of conservation of energy “the loss in kinetic energy of mass is gain in elastic potential energy by spring”.
Let x be the distance of compression of spring, then the law of conservation of energy
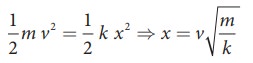
Oscillations of a simple pendulum in SHM and laws of simple pendulum
EXAMPLE 10.13
In simple pendulum experiment, we have used small angle approximation . Discuss the small angle approximation.

For θ in radian, sin θ ≈ θ for very small angles
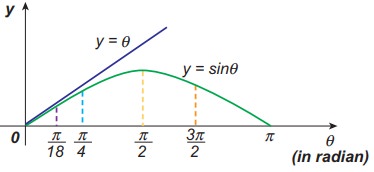
This means that “for θ as large as 10 degrees, sin θ is nearly the same as θ when θ is expressed in radians”. As θ increases in value sinθ gradually becomes different from θ
EXAMPLE 10.14
If the length of the simple pendulum is increased by 44% from its original length, calculate the percentage increase in time period of the pendulum.
Solution

Solved Example Problems for Energy in Simple Harmonic Motion
EXAMPLE 10.15
Write down the kinetic energy and total energy expressions in terms of linear momentum, For one-dimensional case.
Solution
Kinetic energy is KE= 1/2 mvx2
Multiply numerator and denominator by m
KE= [1/2m] m2 vx2 = [1/2m] (mvx )2 = [1/2m] px2
where, px is the linear momentum of the particle executing simple harmonic motion.
Total energy can be written as sum of kinetic energy and potential energy, therefore, from equation (10.73) and also from equation (10.75), we get
E= KE +U( x) = [1/2m] px2 + 1/2 mω2 x2 = constant
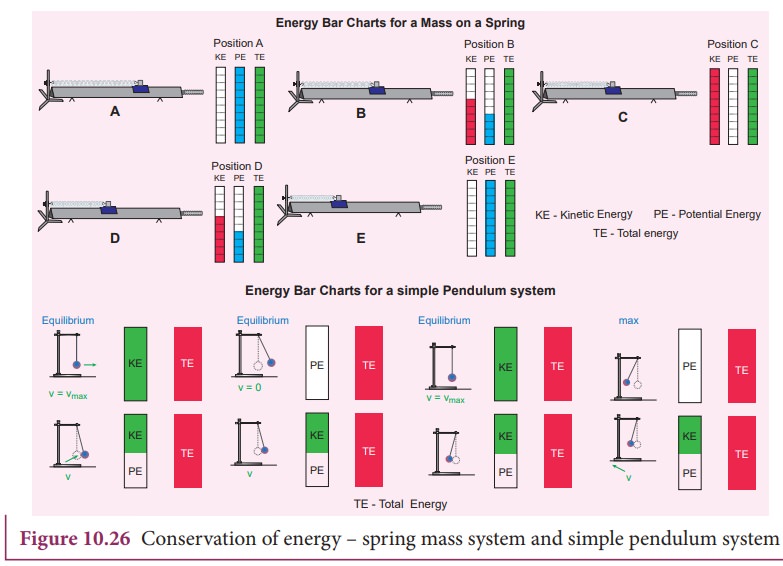
EXAMPLE 10.16
Compute the position of an oscillating particle when its kinetic energy and potential energy are equal.
Solution
Since the kinetic energy and potential energy of the oscillating particle are equal,
1/2 mω 2 (A2 − x 2 ) = 1/2 mω2 x2
A2 − x2 = x2
![]()
![]() 2x2 = A2
2x2 = A2
x = ±A/√2
Related Topics