Oscillations | Physics - Solved Example Problems for Linear Simple Harmonic Oscillator (LHO) | 11th Physics : UNIT 10 : Oscillations
Chapter: 11th Physics : UNIT 10 : Oscillations
Solved Example Problems for Linear Simple Harmonic Oscillator (LHO)
Vertical oscillations of a spring
EXAMPLE 10.8
A spring balance has a scale which ranges from 0 to 25 kg and the length of the scale is 0.25m. It is taken to an unknown planet X where the acceleration due to gravity is 11.5 m s−1. Suppose a body of mass M kg is suspended in this spring and made to oscillate with a period of 0.50 s. Compute the gravitational force acting on the body.
Solution
Let us first calculate the stiffness constant of the spring balance by using equation (10.29),
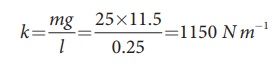
The time period of oscillations is given by T=2π√M/√k, , where M is the mass of the body.
Since, M is unknown, rearranging, we get
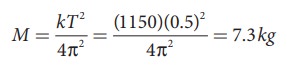
The gravitational force acting on the body is W = Mg = 7.3 × 11.5 = 83.95 N ≈ 84 N
Combinations of springs
EXAMPLE 10.9
Consider two springs whose force constants are 1 N m−1 and 2 N m−1 which are connected in series. Calculate the effective spring constant (ks ) and comment on ks .
Solution
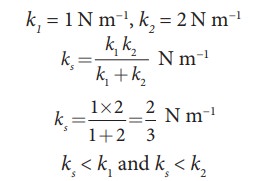
ks < k1 and ks < k
Therefore, the effective spring constant is lesser than both k1 and k2.
EXAMPLE 10.10
Consider two springs with force constants 1 N m−1 and 2 N m−1 connected in parallel. Calculate the effective spring constant (kp ) and comment on kp.
Solution
k1 = 1 N m−1, k2 = 2 N m−1
kp = k1 + k2 N m−1
kp = 1 + 2 = 3 N m−1
kp > k1 and kp > k2
Therefore, the effective spring constant is greater than both k1 and k2.
EXAMPLE 10.11
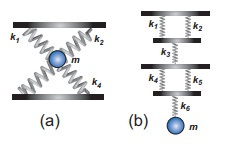
Calculate the equivalent spring constant for the following systems and also compute if all the spring constants are equal:
Solution
a. Since k1 and k2 are parallel, ku = k1 + k2 Similarly, k3 and k4 are parallel, therefore, kd = k3 + k4
But ku and kd are in series,
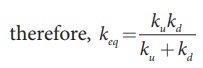
If all the spring constants are equal then, k1 = k2 = k3 = k4 = k
Which means, ku = 2k and kd = 2k
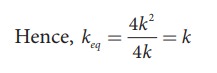
b. Since k1 and k2 are parallel, kA = k1 + k2 Similarly, k4 and k5 are parallel, therefore, kB = k4 + k5
But kA, k3, kB, and k6 are in series,
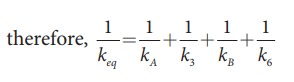
If all the spring constants are equal then, k1 = k2 = k3 = k4 = k5 = k6 = k which means, kA = 2k and kB = 2k
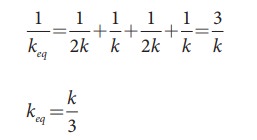
keq = k/3
EXAMPLE 10.12
A mass m moves with a speed v on a horizontal smooth surface and collides with a nearly massless spring whose spring constant is k. If the mass stops after collision, compute the maximum compression of the spring.
Solution
When the mass collides with the spring, from the law of conservation of energy “the loss in kinetic energy of mass is gain in elastic potential energy by spring”.
Let x be the distance of compression of spring, then the law of conservation of energy
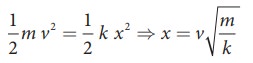
Oscillations of a simple pendulum in SHM and laws of simple pendulum
EXAMPLE 10.13
In simple pendulum experiment, we have used small angle approximation . Discuss the small angle approximation.

For θ in radian, sin θ ≈ θ for very small angles
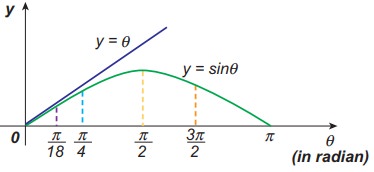
This means that “for θ as large as 10 degrees, sin θ is nearly the same as θ when θ is expressed in radians”. As θ increases in value sinθ gradually becomes different from θ
EXAMPLE 10.14
If the length of the simple pendulum is increased by 44% from its original length, calculate the percentage increase in time period of the pendulum.
Solution

Related Topics