Chapter: 11th Physics : UNIT 10 : Oscillations
Oscillations of a simple pendulum in SHM and laws of simple pendulum
Oscillations of a simple pendulum in SHM and laws of simple pendulum
Simple pendulum
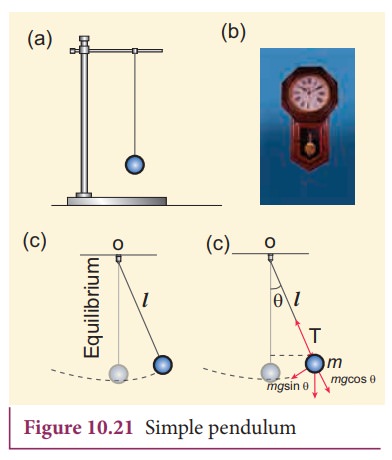
A pendulum is a mechanical system which exhibits periodic motion. It has a bob with mass m suspended by a long string (assumed to be massless and inextensible string) and the other end is fixed on a stand as shown in Figure 10.21 (a). At equilibrium, the pendulum does not oscillate and hangs vertically downward. Such a position is known as mean position or equilibrium position. When a pendulum is displaced through a small displacement from its equilibrium position and released, the bob of the pendulum executes to and fro motion. Let l be the length of the pendulum which is taken as the distance between the point of suspension and the centre of gravity of the bob. Two forces act on the bob of the pendulum at any displaced position, as shown in the Figure 10.21 (d),
![]()
![]() (i) The gravitational force acting on the body (
(i) The gravitational force acting on the body ( 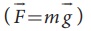 ) which acts vertically downwards.
) which acts vertically downwards.
(ii) The tension in the string ![]() which acts along the string to the point of suspension.
which acts along the string to the point of suspension.
Resolving the gravitational force into its components:
a. Normal component: The component along the string but in opposition to the direction of tension, Fas = mg cosθ.
b. Tangential component: The component perpendicular to the string i.e., along tangential direction of arc of swing, Fps = mg sinθ.
Therefore, The normal component of the force is, along the string,
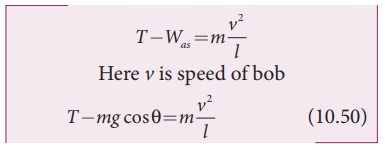
From the Figure 10.21, we can observe that the tangential component Wps of the gravitational force always points towards the equilibrium position i.e., the direction in which it always points opposite to the direction of displacement of the bob from the mean position. Hence, in this case, the tangential force is nothing but the restoring force. Applying Newton’s second law along tangential direction, we have
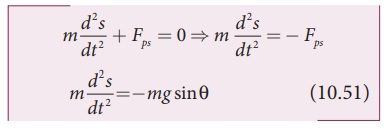
where, s is the position of bob which is measured along the arc. Expressing arc length in terms of angular displacement i.e.,

Substituting equation (10.53) in equation (10.51), we get

Because of the presence of sin θ in the above differential equation, it is a non-linear differential equation (Here, homogeneous second order). Assume “the small oscillation approximation”, sin θ ≈ θ, the above differential equation becomes linear differential equation.

This is the well known oscillatory differential equation. Therefore, the angular frequency of this oscillator (natural frequency of this system) is

Laws of simple pendulum
The time period of a simple pendulum
a. Depends on the following laws
(i) Law of length
For a given value of acceleration due to gravity, the time period of a simple pendulum is directly proportional to the square root of length of the pendulum.

(ii) Law of acceleration
For a fixed length, the time period of a simple pendulum is inversely proportional to square root of acceleration due to gravity.

b. Independent of the following factors
(i) Mass of the bob
The time period of oscillation is independent of mass of the simple pendulum. This is similar to free fall. Therefore, in a pendulum of fixed length, it does not matter whether an elephant swings or an ant swings. Both of them will swing with the same time period.
(ii) Amplitude of the oscillations
For a pendulum with small angle approximation (angular displacement is very small), the time period is independent of amplitude of the oscillation.
EXAMPLE 10.13
In simple pendulum experiment, we have used small angle approximation . Discuss the small angle approximation.

For θ in radian, sin θ ≈ θ for very small angles
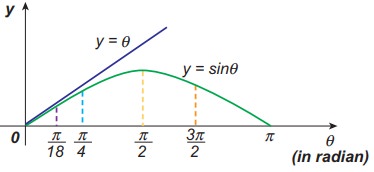
This means that “for θ as large as 10 degrees, sin θ is nearly the same as θ when θ is expressed in radians”. As θ increases in value sinθ gradually becomes different from θ
Pendulum length due to effect of temperature
Suppose the suspended wire is affected due to change in temperature. The rise in temperature affects length by
l = lo (1 + α ∆t)
where lo is the original length of the wire and l is final length of the wire when the temperature is raised. Let ∆t is the change in temperature and α is the co-efficient of linear expansion.
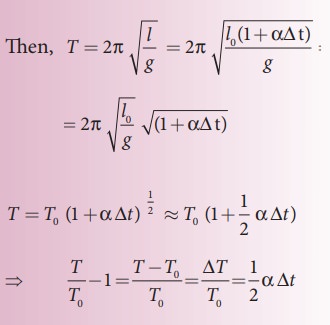
where ∆T is the change in time period due to the effect of temperature and T0 is the time period of the simple pendulum with original length l0.
EXAMPLE 10.14
If the length of the simple pendulum is increased by 44% from its original length, calculate the percentage increase in time period of the pendulum.
Solution

Oscillation of liquid in a U-tube:
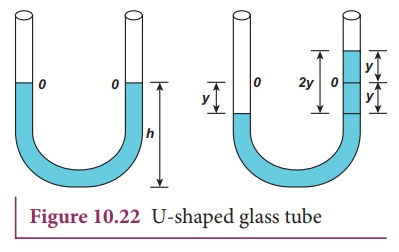
Consider a U-shaped glass tube which consists of two open arms with uniform cross-sectional area A. Let us pour a non-viscous uniform incompressible liquid of density ρ in the U-shaped tube to a height h as shown in the Figure 10.22. If the liquid and tube are not disturbed then the liquid surface will be in equilibrium position O. It means the pressure as measured at any point on the liquid is the same and also at the surface on the arm (edge of the tube on either side), which balances with the atmospheric pressure. Due to this the level of liquid in each arm will be the same. By blowing air one can provide sufficient force in one arm, and the liquid gets disturbed from equilibrium position O, which means, the pressure at blown arm is higher than the other arm. This creates difference in pressure which will cause the liquid to oscillate for a very short duration of time about the mean or equilibrium position and finally comes to rest.
Time period of the oscillation is
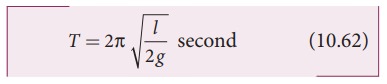
Related Topics