Physics - Kinetic Theory of Gases: Important Questions | 11th Physics : UNIT 9 : Kinetic Theory of Gases
Chapter: 11th Physics : UNIT 9 : Kinetic Theory of Gases
Kinetic Theory of Gases: Important Questions
Short answer questions
1. What is the
microscopic origin of pressure?
2. What is the
microscopic origin of temperature?
3. Why moon has no
atmosphere?
4. Write the expression
for rms speed, average speed and most probable speed of a gas molecule.
5. What is the relation
between the average kinetic energy and pressure?
6. Define the term
degrees of freedom.
7. State the law of
equipartition of energy.
8. Define mean free
path and write down its expression.
9. Deduce Charles’ law
based on kinetic theory.
10. Deduce Boyle’s law
based on kinetic theory.
11. Deduce Avogadro’s
law based on kinetic theory.
12. List the factors
affecting the mean free path.
13. What is the reason
for Brownian motion?
Long answer questions
1. Write down the
postulates of kinetic theory of gases.
2. Derive the
expression of pressure exerted by the gas on the walls of the container.
3. Explain in detail
the kinetic interpretation of temperature.
4. Describe the total
degrees of freedom for monoatomic molecule, diatomic molecule and triatomic
molecule.
5. Derive the ratio of
two specific heat capacities of monoatomic, diatomic and triatomic molecules
6. Explain in detail
the Maxwell Boltzmann distribution function.
7. Derive the
expression for mean free path of the gas.
8. Describe the
Brownian motion.
Numerical Problems
1. A fresh air is composed of nitrogen N2(78%) and oxygen O2(21%). Find the rms speed of N2 and O2 at 20°C.
Solution:
For Nitrogen,
Molar mass m = 0.0280 kg/mol
Temperature T = 20°C = 20 + 273 = 293K
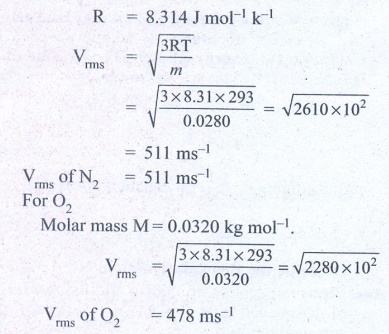
Ans: For vrms = 511 m s-1
For O2vrms = 478 m s-1
2. If the rms speed of methane gas in the Jupiter’s atmosphere is 471.8 m s-1, show that the surface temperature of Jupiter is sub-zero.
Solution:
RMS speed of methane gas = 471.8 ms-1 =Vrms
Sub-zero temperature Molar mass of methane gas
= 16.04 × 10-3 kg mol-1
Surface temperature of Jupiter T = ?
Gas constant R =8.31
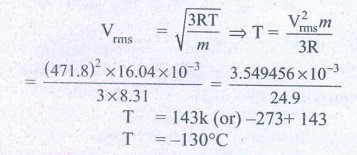
Ans: -130°C
3. Calculate the temperature at which the rms velocity of a gas triples its value at S.T.P.

Ans: T1 = 273 K, T2 = 2457 K
4. A gas is at temperature 80°C and pressure 5 × 10-10N m-2. What is the number of molecules per m3 if Boltzmann’s constant is 1.38 × 10-23 J K-1
Solution:
Temperature of gas T = 80°C = 80 + 273 = 353K
Pressure of gas P = 5 × 10-10 Nm-2
Boltzmann’s constant k = 1.38 × 10-23 Jk-1
Volume of gas V = 1 m3
No. of molecules n = ?
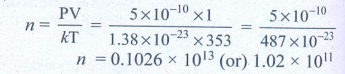
Ans: 1.02 × 1011
5. From kinetic theory of gases, show that Moon cannot have an atmosphere (Assume k = 1.38 × 10-23 J K-1 Temperature T=0°C=273K).
Ans: vescape = vrms= 1.86 km s-1
6. If 1020 oxygen molecules per second strike 4 cm2 of wall at an angle of 30° with the normal when moving at a speed of 2 × 103 m s-1, find the pressure exerted on the wall. (mass of 1 atom = 1.67 × 10-27 kg)
Solution
Mass of 1 O2 atom = 2.67 × 10-26 kg
Mass of 1020 O2 atom = 2.67 × 10-26 kg
= 26.72 × 10-27 × 1020
Momentum P = mv
= 26.72 × 10-7 × 8 × 2 × 103
= 427.5 × 10-4 kgm s-1
Component of momentum normal to wall is 30°
= 427.5 ×10-4 × cos 30° .

Ans: 92.4 N m-2
7. During an adiabatic process, the pressure of a mixture of monatomic and diatomic gases is found to be proportional to the cube of the temperature. Find the value of γ = (Cp/CV)
Solution

Ans: 3/2
8. Calculate the mean free path of air molecules at STP. The diameter of N2 and O2 is about 3 × 10-10 m
Solution

Ans: λ≈9 × 10-8 m
9. A gas made of a mixture of 2 moles of oxygen and 4 moles of argon at temperature T. Calculate the energy of the gas in terms of RT. Neglect the vibrational modes.

Ans: 11RT
10. Estimate the total number of air molecules in a room of capacity 25 m3 at a temperature of 27°C.
Solution:
Volume of the room V = 25.0m3
Temperature of the room T = 27°C = 300K
Pressure in the room P = estimate
= 1 × 1.013 × 105 Pa
The ideal gas equation relating pressure (P), volume (v) absolute temperature (T) can be written is
PV = KB NT
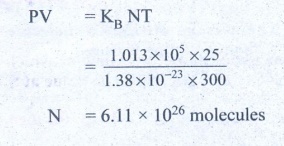
Ans: 6.1 × 1026 molecules
Related Topics