Kinetic Theory of Gases | Physics - Long Questions and Answer | 11th Physics : UNIT 9 : Kinetic Theory of Gases
Chapter: 11th Physics : UNIT 9 : Kinetic Theory of Gases
Long Questions and Answer
Kinetic Theory of Gases | Physics
Long answer questions
1. Write down the postulates of kinetic theory of gases.
●
All the molecules of a gas are identical, elastic spheres.
●
The molecules of different gases are different.
●
The number of molecules in a gas is very large and the average separation
between them is larger than size of the gas molecules.
●
The molecules of a gas are in a state of continuous random motion.
●
The molecules collide with one another and also with the walls of the
container.
●
These collisions are perfectly elastic so that there is no loss of kinetic
energy during collisions.
●
Between two successive collisions, a molecule moves with uniform velocity.
●
The molecules do not exert any force of attraction or repulsion on each other
except during collision. The molecules do not possess any potential energy and
the energy is wholly kinetic.
●
The collisions are instantaneous. The time spent by a molecule in each
collision is very small compared to the time elapsed between two consecutive
collisions.
●
These molecules obey Newton's laws of motion even though they move randomly.
2. Derive the expression of pressure exerted by the gas on the walls of the container.
●
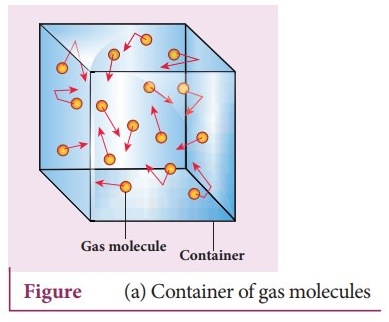
Consider a monatomic gas of N molecules each having a mass m inside a cubical
container of side l. The molecules of the gas are in random motion.
●
They collide with each other and also with the walls of the container. As the
collisions are elastic in nature, there is no loss of energy, but a change in
momentum occurs.
●
The molecules of the gas exert pressure on the walls of the container due to
collision on it.
●
During each collision, the molecules impart certain momentum to the wall. Due
to transfer of momentum, the walls experience a continuous force.
●
The force experienced per unit area of the walls of the container determines
the pressure exerted by the gas.
●
It is essential to determine the total momentum transferred by the molecules in
a short interval of time.
●
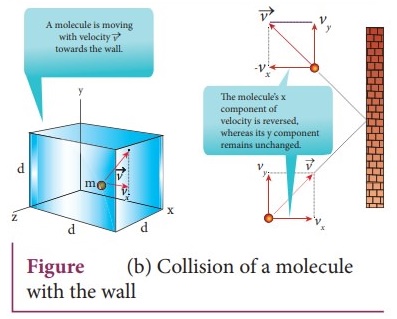
A molecule of mass m moving with a velocity v̄ having components (vx,
vy, vz) hits the right side wall.
●
The collision is elastic, the particle rebounds with same speed and its
x-component is reversed.
●
This is shown in the Figure (b). The components of velocity of the molecule
after collision are (−vx, vy, vz).
The
x-component of momentum of the molecule before collision = mvx.
The
x-component of momentum of the molecule after collision = −mvx
●
The change in momentum of the molecule in x direction = Final momentum − initial
momentum = − mvx − mvx = −2 mvx According to
law of conservation of linear momentum, the change in momentum of the wall = 2mvx
●
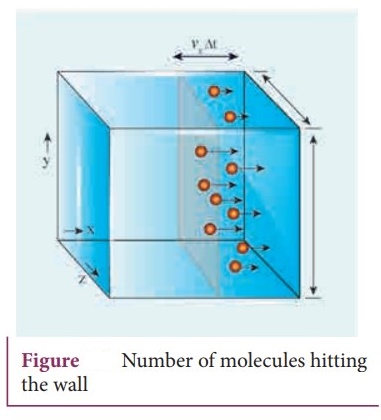
The number of molecules hitting the right side wall in a small interval of time
Δt is calculated as follows.
●
The molecules within the distance of vxΔt from the right side wall
and moving towards the right will hit the wall in the time interval Δt.
● The number of molecules that will hit the right side wall in a time interval Δt is equal to the product of volume (Avx Δt) and number density of the molecules (n).
●
Here A is area of the wall and n is number of molecules per unit volume (N/V).
The number density is the same throughout the cube.
●
Not all the n molecules will move to the right, therefore on an average only
half of the n molecules move to the right and the other half moves towards left
side.
●
The number of molecules that hit the right side wall in a time interval ∆t
= n / 2 Avx∆t ………. (1)
●
In the same interval of time ∆t, the total momentum transferred by the
molecules.
∆p
= n/2 Avx ∆t × 2mvx= Av2x
mnΔt …………(2)
●
From Newton's second law, the change in momentum in a small interval of time
gives rise to force. The force exerted by the molecules on the wall (in
magnitude)
F
= ∆p / Δt = nmAv2x ……….. (3)
Pressure,
P = force divided by the area of the wall
P
= F / A = nmv2x ……………..(4)
●
Since all the molecules are moving completely in random manner, they do not
have same speed. So we can replace the term vx2 by
the average 
in equation.
………….
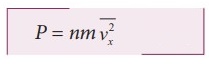(5)
●
Since the gas is assumed to move in random direction, it has no preferred
direction of motion (the effect of gravity on the molecules is neglected). The
molecule has same average speed in all the three direction. So,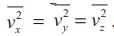 
. The
mean square speed is written as
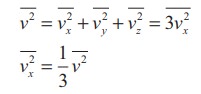
Using this in equation (5), we get,
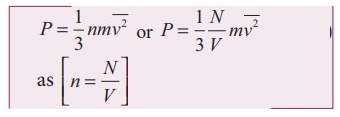
3. Explain in detail the kinetic interpretation of temperature.
1) To
understand the microscopic origin of temperature in the same way,
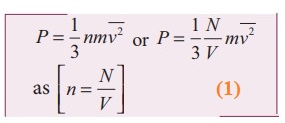
Rewrite the equation
●
Comparing the equation (2) with ideal gas equation PV=NKT,
●
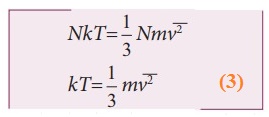
Multiply the above equation by 3/2 on both sides,
●
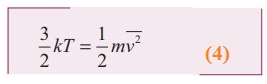
R.H.S of the equation (3) is called average kinetic energy of a single molecule 
The
average kinetic energy per molecule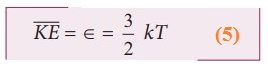 
●
Equation (4) implies that the temperature of a gas is a measure of the average
translational kinetic energy per molecule of the gas.
●
Equation (4) implies that the temperature of a gas is a measure of the average
translational kinetic energy per molecule of the gas.
●
The average kinetic energy of each molecule depends only on temperature of the
gas not on mass of the molecule.
●
If the temperature of an ideal gas is measured using thermometer, the average
kinetic energy of each molecule can be calculated without seeing the molecule
through naked eye.
●
By multiplying the total number of gas molecules with average kinetic energy of
each molecule, the internal energy of the gas is obtained.
Internal
energy of ideal gas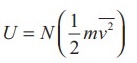 
By
using equation (4)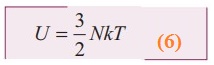 
………… 6
From
equation (6). The internal energy of an ideal gas depends only on absolute
temperature and is independent of pressure and volume.
4. Describe the total degrees of freedom for monoatomic molecule, diatomic molecule and triatomic molecule.
Mono-atomic
molecule : A monoatomic molecule by virtue of its nature has only three
translational degrees of freedom. Therefore f = 3
Example: Helium,
Neon, Argon
Diatomic
molecule : There are two cases.
1.
At Normal temperature:
●
A molecule of a diatomic gas consists of two atoms bound to each other by a
force of attraction.
●
The molecule can be regarded as a system of two point masses fixed at the ends
of a massless elastic spring.
●
The center of mass lies in the center of the diatomic molecule.
●
So, the motion of the center of mass requires three translational degrees of
freedom (figure a). The diatomic molecule can rotate about three mutually
perpendicular axes (figure b).
●
But the moment of inertia about its own axis of rotation is negligible (about y
axis in the figure).
●
Therefore, it has only two rotational degrees of freedom (one rotation is about
Z axis and another rotation is about Y axis). Therefore totally there are five
degrees of freedom.
f = 5
2.
At High Temperature:
●
At a very high temperature such as 5000 K, the diatomic molecules possess
additional two degrees of freedom due to vibrational motion [one due to kinetic
energy of vibration and the other is due to potential energy] (Figure c). So
totally there are seven degrees of freedom.
f = 7
Examples:
Hydrogen, Nitrogen, Oxygen.
3.
Triatomic molecules:
●
There are two cases.
●
Linear triatomic molecule In this type, two atoms lie on either side of the
central atom.
●
Linear triatomic molecule has three translational degrees of freedom. It has
two rotational degrees of freedom because it is similar to diatomic molecule
except there is an additional atom at the center.
●
At normal temperature, linear triatomic molecule will have five degrees of
freedom.
●
At high temperature it has two additional vibrational degrees of freedom. So a
linear triatomic molecule has seven degrees of freedom.
Example: Carbon
dioxide.
4.
Non-linear triatomic molecule:
●
The three atoms lie at the vertices of a triangle.
●
It has three translational degrees of freedom and three rotational degrees of
freedom about three mutually orthogonal axes.
●
The total degrees of freedom, f = 6
Example: Water,
Sulphurdioxide.
5. Derive the ratio of two specific heat capacities of monoatomic, diatomic and triatomic molecules
Application
of law of equipartition energy in specific heat of a gas
●
Meyer's relation CP − CV = R connects the two specific
heats for one mole of an ideal gas.
●
Equipartition law of energy is used to calculate the value of CP − CV
and the ratio between them γ = CP / CV.
Here γ is called adiabatic exponent.
i)
Monatomic molecule:
●
Average kinetic energy of a molecule = [3/2 kT]
●
Total energy of a mole of gas = 3/2 kT × NA = 3/2 RT
●
For one mole, the molar specific heat at constant volume = CV
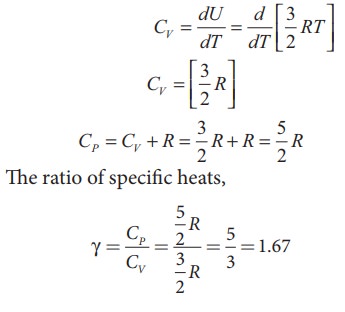
ii)
Diatomic molecule:
●
Average kinetic energy' of a diatomic molecule at low temperature = 5/2 kT
●
Total energy of one mole of gas = 5/2 kT × NA = 5/2 RT
●
For one mole, Specific heat at constant volume.
CV
= dU / dT = [5/2RT ] ; CV =
5/2 R
●
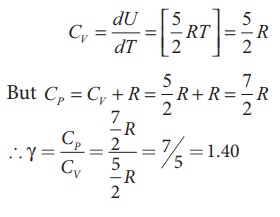
Energy of a diatomic molecule at high temperature is equal to
●
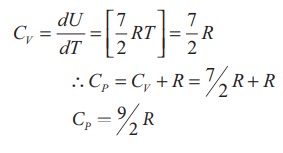
The CV and CP are higher for diatomic molecules than the
mono atomic molecules. It implies that to increase the temperature of diatomic
gas molecules by 1°C it require more heat energy than monoatomic molecules,
The
ratio of Specific heats, γ = CP / CV
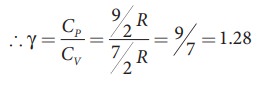
= [9/2 R ] / [ 7/2 R ] = 9/7 =
1.28
iii)
Triatomic molecule:
a) Linear molecule
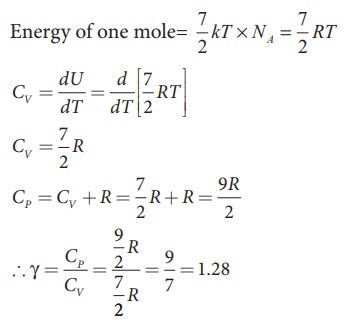
The
ratio of specific heats, γ = CP / CV
= [ 9/2 R ] / [ 7/2 R ] = 9/7
γ = 1.28
b)
Non-linear molecule
Energy
of a mole = 6/2 kT × NA = 6/2 RT = 3RT
CV = dU
/ dT = 3R
But,
CP = CV + R; = 3R + R = 4R
The
ratio of specific heats, γ = CP / CV ;
γ
= CP / CV =
4R / 3R = 4/3 = 1.33
According
to kinetic theory model of gases, the specific heat capacity at constant volume
and constant pressure are independent of temperature. But in reality it is not
sure. The specific heat capacity varies with the temperature.
6. Explain in detail the Maxwell Boltzmann distribution function.
●
The air molecules are moving in random directions.
●
The speed of each molecule is not the same even though macroscopic parameters
like temperature and pressure are fixed.
●
Each molecule collides with every other molecule and they exchange their speed.
●
In this scenario we can find the number of gas molecules that move with the
speed of 5 m s−1 to 10 ms−1 or 10 ms−1 to 15
ms−1 etc.
●
To find how many gas molecules have the range of speed from v to v + dv. This
is given by Maxwell's speed distribution function.
Nv = 4πN
( m / 2πkT)3/2 v2e mv2/2kT
The
number of molecules having speeds ranging from υ to υ + dυ
equals the area of the rectangle, Nv + dυ.
●
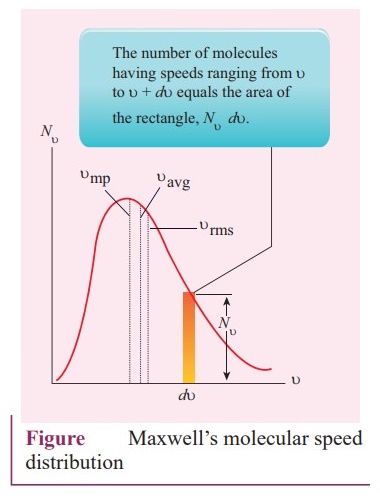
For a given temperature the number of molecules having lower speed increases
parabolically but decreases exponentially after reaching most probable speed.
●
The speed is greatest among the three.
●
The area under the graph will give the total number of gas molecules in the
system.
●
As temperature increases, the peak of the curve is shifted to the right. It
implies that the average speed of each molecule will increase. But the area
under each graph is same since it represents the total number of gas molecules.
7. Derive the expression for mean free path of the gas.
Expression
for mean free path:
●
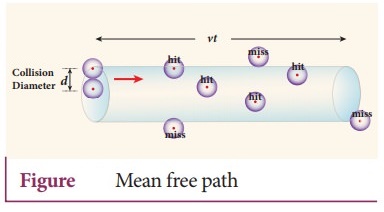
The molecules of a gas are in random motion and they collide with each other.
●
Between two successive collisions, a molecule moves along a straight path with
uniform velocity.
●
This path is called mean free path. Consider a system of molecules each with
diameter d. Let n be the number of molecules per unit volume.
●
Assume that only one molecule is in motion and all others are at rest.
●
If a molecule moves with average speed v in a time t, the distance travelled is
vt. In this time t, consider the molecule to move in an imaginary cylinder of
volume nd2vt.
●
It collides with any molecule whose center is within this cylinder. Therefore,
the number of collisions is equal to the number of molecules in the volume of
the imaginary cylinder.
●
It is equal to πd2vtn. The total path length divided by the number
of collisions in time t is the mean free path.
Mean
free path, λ = distance travelled / Number of collisions ;
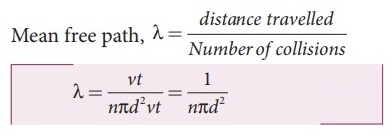
λ
= vt / nπd2vt = 1 / nπd2 …….. (1)
●
Only one molecule is moving at a time and other molecules are at rest, in
actual practice all the molecules are in random motion.
●
So the average relative speed of one molecule with respect to other molecules
has to be taken into account.
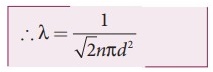………….(2)
●
The equation (1) implies that the mean free path is inversely proportional to
number density.
●
When the number density increases the molecular collisions increases so it
decreases the distance travelled by the molecule before collisions.
Case
1 : Rearranging the equation (2) using ‘m' (mass of the molecule)
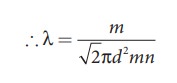
But
mn = mass per unit volume = ρ (density of the gas)
Substituting
n = P / kT in equation (2), we get kT
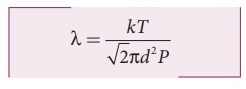
8. Describe the Brownian motion.
●
Brownian motion is due to the bombardment of suspended particles by molecules
of the surrounding fluid.
●
According to kinetic theory, any particle suspended in a liquid or gas is
continuously bombarded from all the directions so that the mean free path is
almost negligible.
●
This leads to the motion of the particles in a random and zig-zag manner.
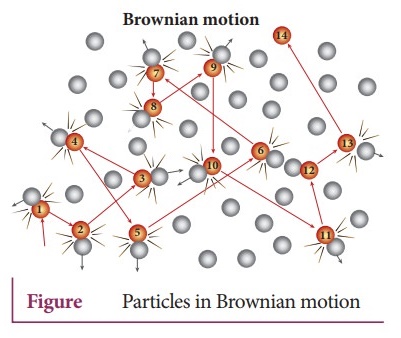
Factors
affecting Brownian motion:
●
Brownian motion increases with increasing temperature.
●
Brownian motion decreases with bigger particle size, high viscosity and density
of the liquid (or) gas.
Related Topics