Kinetic interpretation of temperature

Kinetic interpretation of temperature

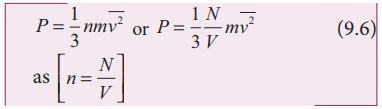
To understand the microscopic origin of temperature in the same way,

Rewrite the equation (9.6)

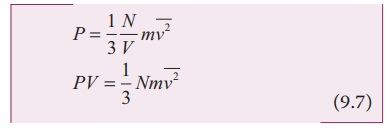
Comparing the equation (9.7) with ideal gas equation PV=NkT,

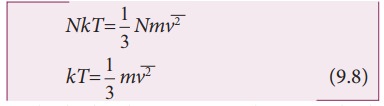
Multiply the above equation by 3/2 on both sides,

R.H.S of the equation (9.9) is called average kinetic energy of a single molecule .

The average kinetic energy per molecule

Equation (9.9 ) implies that the temperature of a gas is a measure of the average translational kinetic energy per molecule of the gas.

Equation 9.10 is a very important result from kinetic theory of gas. We can infer the following from this equation.

(i) The average kinetic energy of the molecule is directly proportional to absolute temperature of the gas. The equation (9.9) gives the connection between the macroscopic world (temperature) to microscopic world (motion of molecules).

(ii) The average kinetic energy of each molecule depends only on temperature of the gas not on mass of the molecule. In other words, if the temperature of an ideal gas is measured using thermometer, the average kinetic energy of each molecule can be calculated without seeing the molecule through naked eye.

By multiplying the total number of gas molecules with average kinetic energy of each molecule, the internal energy of the gas is obtained.

Internal energy of ideal gas U =

From equation (9.11), we understand that the internal energy of an ideal gas depends only on absolute temperature and is independent of pressure and volume.

EXAMPLE 9.1

A football at 27°C has 0.5 mole of air molecules. Calculate the internal energy of air in the ball.

Solution

The internal energy of ideal gas = 3/2 NkT. The number of air molecules is given in terms of number of moles so, rewrite the expression as follows

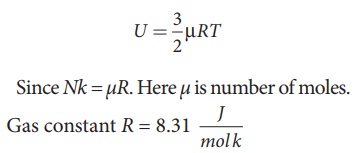
Temperature T =273+27=300K

U = 3/2 × 0.5 × 8.31 × 300 = 1869.75J

This is approximately equivalent to the kinetic energy of a man of 57 kg running with a speed of 8 m s^-1.