Law of Equipartition of Energy

LAW OF EQUIPARTITION OF ENERGY

We have seen in Section 9.2.1 that the average kinetic energy of a molecule moving in x direction is

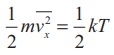
Similarly, when the motion is in y direction,

According to kinetic theory, the average kinetic energy of system of molecules in thermal equilibrium at temperature T is uniformly distributed to all degrees of freedom (x or y or z directions of motion) so that each degree of freedom will get 1/2 kT of energy. This is called law of equipartition of energy.

Average kinetic energy of a monatomic molecule (with f=3) =

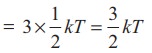
Average kinetic energy of diatomic molecule at low temperature (with f = 5)

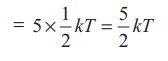
Average kinetic energy of a diatomic molecule at high temperature (with f =7)

Average kinetic energy of linear triatomic molecule (with f = 7) =

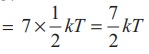
Average kinetic energy of nonlinear tri atomic molecule (with f = 6) =

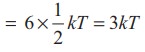
Application of law of equipartition energy in specific heat of a gas

Meyer’s relation C_P − C_V = R connects the two specific heats for one mole of an ideal gas.

Equipartition law of energy is used to calculate the value of C_P − C_V and the ratio between them γ = C_P / C_V.

Here γ is called adiabatic exponent.

i)  Monatomic molecule

Average kinetic energy of a molecule

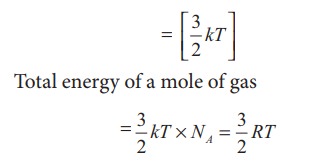
For one mole, the molar specific heat at constant volume

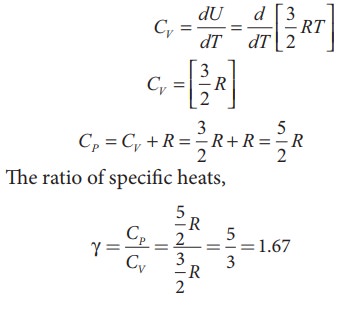
ii)  Diatomic molecule

Average kinetic energy of a diatomic molecule at low temperature = 5/2kT

Total energy of one mole of gas

(Here, the total energy is purely kinetic)

For one mole Specific heat at constant volume

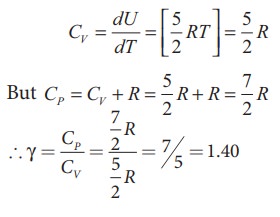
Energy of a diatomic molecule at high temperature is equal to 7/2RT

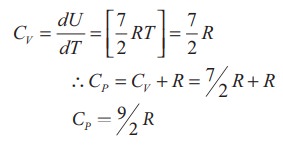
Note that the C_V and C_P are higher for diatomic molecules than the mono atomic molecules. It implies that to increase the temperature of diatomic gas molecules by 1°C it require more heat energy than monoatomic molecules.

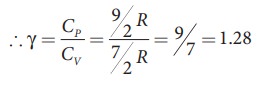
iii)  Triatomic molecule

a)  Linear molecule

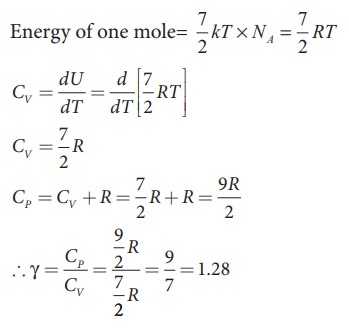
b)  Non-linear molecule

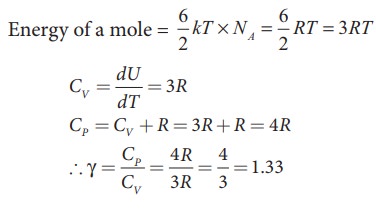
Note that according to kinetic theory model of gases the specific heat capacity at constant volume and constant pressure are independent of temperature. But in reality it is not sure. The specific heat capacity varies with the temperature.

EXAMPLE 9.5

Find the adiabatic exponent γ for mixture of μ ₁ moles of monoatomic gas and μ₂ moles of a diatomic gas at normal temperature.

Solution