Root mean square speed

Root mean square speed (v_rms)

Root mean square speed (v_rms) is defined as the square root of the mean of the square of speeds of all molecules. It is denoted by v_rms = √v²

Equation (9.8) can be re-written as,

From the equation (9.18) we infer the following

(i) rms speed is directly proportional to square root of the temperature and inversely proportional to square root of mass of the molecule. At a given temperature the molecules of lighter mass move faster on an average than the molecules with heavier masses.

Example: Lighter molecules like hydrogen and helium have high ‘v_rms’ than heavier molecules such as oxygen and nitrogen at the same temperature.

(ii) Increasing the temperature will increase the r.m.s speed of molecules

We can also write the v_rms in terms of gas constant R. Equation (9.18) can be rewritten as follows

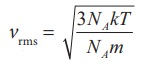
Where N_A is Avogadro number.

Since N_Ak = R and N_Am = M (molar mass)

The root mean square speed or r.m.s speed

The equation (9.6) can also be written in terms of rms speed

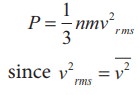
Impact of v_rms in nature:

1. Moon has no atmosphere.

The escape speed of gases on the surface of Moon is much less than the root mean square speeds of gases due to low gravity. Due to this all the gases escape from the surface of the Moon.

2. No hydrogen in Earth’s atmosphere.

As the root mean square speed of hydrogen is much less than that of nitrogen, it easily escapes from the earth’s atmosphere.

In fact, the presence of nonreactive nitrogen instead of highly combustible hydrogen deters many disastrous consequences.

EXAMPLE 9.2

A room contains oxygen and hydrogen molecules in the ratio 3:1. The temperature of the room is 27°C. The molar mass of 0₂ is 32 g mol-1 and for H₂ 2 g mol^-1. The value of gas constant R is 8.32 J mol^-1K^-1

Calculate

(a) rms speed of oxygen and hydrogen molecule

(b) Average kinetic energy per oxygen molecule and per hydrogen molecule

(c) Ratio of average kinetic energy of oxygen molecules and hydrogen molecules

Solution

(a) Absolute Temperature

T=27°C =27+273=300 K.

Gas constant R=8.32 J mol^-1k^-1

For Oxygen molecule: Molar mass

M=32 gm=32 x 10^-3 kg mol^-1

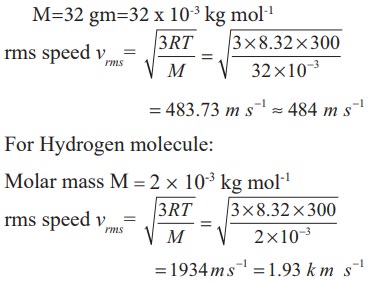
Note that the rms speed is inversely proportional to √M and the molar mass of oxygen is 16 times higher than molar mass of hydrogen. It implies that the rms speed of hydrogen is 4 times greater than rms speed of oxygen at the same temperature.

1934/484 ≈ 4 .

(b) The  average  kinetic  energy  per molecule is 3/2 kT. It depends only on absolute temperature of the gas and is independent of the nature of molecules. Since both the gas molecules are at the same temperature, they have the same average kinetic energy per molecule. k is Boltzmaan constant.

(c) Average  kinetic  energy  of  total oxygen molecules = 3/2 N₀kT where N₀ - number of oxygen molecules in the room

Average  kinetic  energy  of  total hydrogen  molecules = 3/2 N_HkT where N_H - number of hydrogen molecules in the room.

It is given that the number of oxygen molecules is 3 times more than number of hydrogen molecules in the room. So the ratio of average kinetic energy of oxygen molecules with average kinetic energy of hydrogen molecules is 3:1