Chapter: 11th Physics : UNIT 9 : Kinetic Theory of Gases
Solved Example Problems for Physics: Kinetic Theory of Gases
Numerical Problems
1. A fresh air is composed of nitrogen N2(78%) and oxygen O2(21%). Find the rms speed of N2 and O2 at 20°C.
Solution:
For Nitrogen,
Molar mass m = 0.0280 kg/mol
Temperature T = 20°C =
20 + 273 = 293K
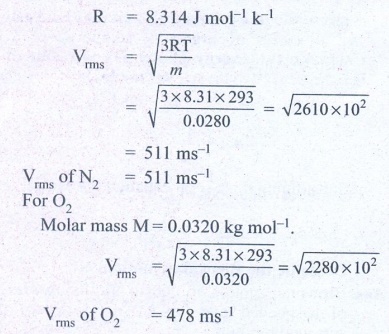
Ans: For vrms = 511 m s-1
For O2vrms = 478 m s-1
2. If the rms speed of methane gas in the Jupiter’s atmosphere is 471.8 m s-1, show that the surface temperature of Jupiter is sub-zero.
Solution:
RMS speed of methane
gas = 471.8 ms-1 =Vrms
Sub-zero temperature
Molar mass of methane gas
= 16.04 × 10-3 kg mol-1
Surface temperature of
Jupiter T = ?
Gas constant R =8.31
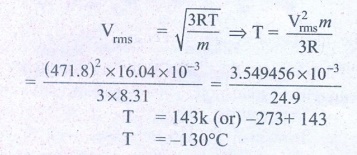
Ans: -130°C
3. Calculate the temperature at which the rms velocity of a gas triples its value at S.T.P.

Ans: T1 = 273 K, T2 = 2457 K
4. A gas is at temperature 80°C and pressure 5 × 10-10N m-2. What is the number of molecules per m3 if Boltzmann’s constant is 1.38 × 10-23 J K-1
Solution:
Temperature of gas T =
80°C = 80 + 273 = 353K
Pressure of gas P = 5 ×
10-10 Nm-2
Boltzmann’s constant k
= 1.38 × 10-23 Jk-1
Volume of gas V = 1 m3
No. of molecules n = ?

Ans: 1.02 × 1011
5. From kinetic theory of gases, show that Moon cannot have an atmosphere (Assume k = 1.38 × 10-23 J K-1 Temperature T=0°C=273K).
Ans: vescape = vrms= 1.86 km s-1
6. If 1020 oxygen molecules per second strike 4 cm2 of wall at an angle of 30° with the normal when moving at a speed of 2 × 103 m s-1, find the pressure exerted on the wall. (mass of 1 atom = 1.67 × 10-27 kg)
Solution
Mass of 1 O2
atom = 2.67 × 10-26 kg
Mass of 1020
O2 atom = 2.67 × 10-26 kg
= 26.72 × 10-27 × 1020
Momentum P = mv
= 26.72 × 10-7
× 8 × 2 × 103
= 427.5 × 10-4
kgm s-1
Component of momentum
normal to wall is 30°
= 427.5 ×10-4
× cos 30° .

Ans: 92.4 N m-2
7. During an adiabatic process, the pressure of a mixture of monatomic and diatomic gases is found to be proportional to the cube of the temperature. Find the value of γ = (Cp/CV)
Solution

Ans: 3/2
8. Calculate the mean free path of air molecules at STP. The diameter of N2 and O2 is about 3 × 10-10 m
Solution

Ans: λ≈9 × 10-8 m
9. A gas made of a mixture of 2 moles of oxygen and 4 moles of argon at temperature T. Calculate the energy of the gas in terms of RT. Neglect the vibrational modes.

Ans: 11RT
10. Estimate the total number of air molecules in a room of capacity 25 m3 at a temperature of 27°C.
Solution:
Volume of the room V =
25.0m3
Temperature of the room
T = 27°C = 300K
Pressure in the room P
= estimate
= 1 × 1.013 × 105
Pa
The ideal gas equation
relating pressure (P), volume (v) absolute temperature (T) can be written is
PV = KB NT
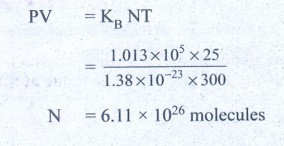
Ans: 6.1 × 1026 molecules
Solved Example Problems: Expression for pressure exerted by a gas
EXAMPLE 9.1
A football at 27°C has 0.5 mole of air molecules. Calculate the internal energy of air in the ball.
Solution
The internal energy of ideal gas = 3/2 NkT. The number of air molecules is given in terms of number of moles so, rewrite the expression as follows
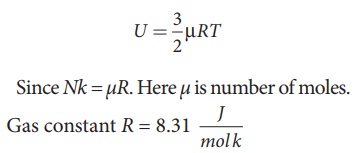
Temperature T =273+27=300K
U = 3/2 × 0.5 × 8.31 × 300 = 1869.75J
This is approximately equivalent to the kinetic energy of a man of 57 kg running with a speed of 8 m s-1.
EXAMPLE 9.2(Root mean square speed)
A room contains oxygen and hydrogen molecules in the ratio 3:1. The temperature of the room is 27°C. The molar mass of 02 is 32 g mol-1 and for H2 2 g mol-1. The value of gas constant R is 8.32 J mol-1K-1
Calculate
(a) rms speed of oxygen and hydrogen molecule
(b) Average kinetic energy per oxygen molecule and per hydrogen molecule
(c) Ratio of average kinetic energy of oxygen molecules and hydrogen molecules
Solution
(a) Absolute Temperature
T=27°C =27+273=300 K.
Gas constant R=8.32 J mol-1k-1
For Oxygen molecule: Molar mass
M=32 gm=32 x 10-3 kg mol-1
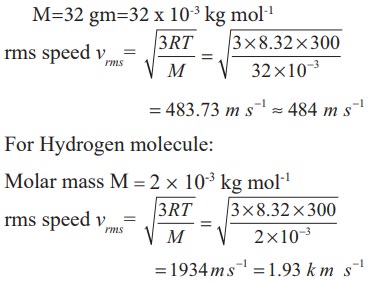
Note that the rms speed is inversely proportional to √M and the molar mass of oxygen is 16 times higher than molar mass of hydrogen. It implies that the rms speed of hydrogen is 4 times greater than rms speed of oxygen at the same temperature.
1934/484 ≈ 4 .
(b) The average kinetic energy per molecule is 3/2 kT. It depends only on absolute temperature of the gas and is independent of the nature of molecules. Since both the gas molecules are at the same temperature, they have the same average kinetic energy per molecule. k is Boltzmaan constant.

(c) Average kinetic energy of total oxygen molecules = 3/2 N0kT where N0 - number of oxygen molecules in the room
Average kinetic energy of total hydrogen molecules = 3/2 NHkT where NH - number of hydrogen molecules in the room.
It is given that the number of oxygen molecules is 3 times more than number of hydrogen molecules in the room. So the ratio of average kinetic energy of oxygen molecules with average kinetic energy of hydrogen molecules is 3:1
EXAMPLE 9.3
Ten particles are moving at the speed of 2, 3, 4, 5, 5, 5, 6, 6, 7 and 9 m s-1. Calculate rms speed, average speed and most probable speed.
Solution
The average speed

The most probable speed is 5 ms-1 because three of the particles have that speed.
EXAMPLE 9.4
Calculate the rms speed, average speed and the most probable speed of 1 mole of hydrogen molecules at 300 K. Neglect the mass of electron.
Solution
The hydrogen atom has one proton and one electron. The mass of electron is negligible compared to the mass of proton.
Mass of one proton = 1.67 × 10−27kg.
One hydrogen molecule = 2 hydrogen atoms = 2 × 1.67 × 10−27kg.
The average speed

Solved Example Problems for Law of Equipartition of Energy
EXAMPLE 9.5
Find the adiabatic exponent γ for mixture of μ 1 moles of monoatomic gas and μ2 moles of a diatomic gas at normal temperature.
Solution

Solved Example Problems for Mean Free Path
EXAMPLE 9.6
An oxygen molecule is travelling in air at 300 K and 1 atm, and the diameter of oxygen molecule is 1.2 × 10−10m. Calculate the mean free path of oxygen molecule.
Solution
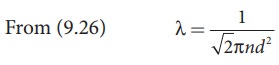
We have to find the number density n By using ideal gas law
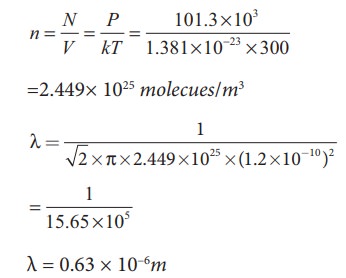
Related Topics