Expression for pressure exerted by a gas

PRESSURE EXERTED BY A GAS

Expression for pressure exerted by a gas

Consider a monatomic gas of N molecules each having a mass m inside a cubical container of side l as shown in the Figure 9.1 (a).

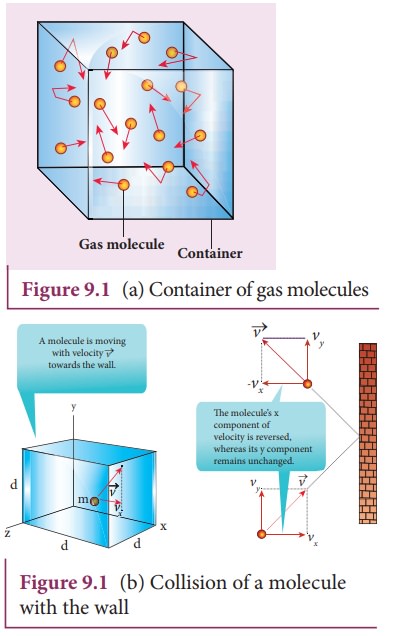
The molecules of the gas are in random motion. They collide with each other and also with the walls of the container. As the collisions are elastic in nature, there is no loss of energy, but a change in momentum occurs.

The molecules of the gas exert pressure on the walls of the container due to collision on it. During each collision, the molecules impart certain momentum to the wall. Due to transfer of momentum, the walls experience a continuous force. The force experienced per unit area of the walls of the container determines the pressure exerted by the gas. It is essential to determine the total momentum transferred by the molecules in a short interval of time.

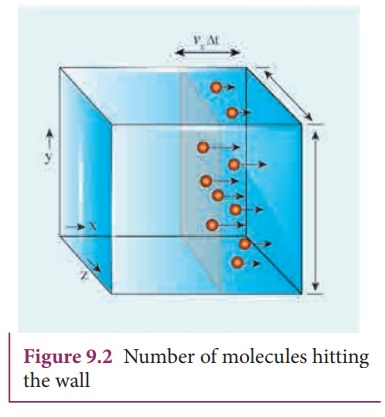
A molecule of mass m moving with a velocity  having components (v_x, v_y, v_z) hits the right side wall. Since we have assumed that the collision is elastic, the particle rebounds with same speed and its x-component is reversed. This is shown in the Figure 9.1 (b). The components of velocity of the molecule after collision are (—v_x, v_y, v_z).

The x-component of momentum of the molecule before collision = mv_x

The x-component of momentum of the molecule after collision = −mv_x

The change in momentum of the molecule in x direction

=Final momentum – initial momentum = −mv_x −mv_x = −2mv_x

According to law of conservation of linear momentum, the change in momentum of the wall = 2mv_x

The number of molecules hitting the right side wall in a small interval of time ∆t is calculated as follows.

The molecules within the distance of v_x∆t from the right side wall and moving towards the right will hit the wall in the time interval ∆t. This is shown in the Figure 9.2. The number of molecules that will hit the right side wall in a time interval ∆t is equal to the product of volume (Av_x∆t) and number density of the molecules (n). Here A is area of the wall and n is number of molecules per unit volume (N/V). We have assumed that the number density is the same throughout the cube.

Not all the n molecules will move to the right, therefore on an average only half of the n molecules move to the right and the other half moves towards left side.

The number of molecules that hit the right side wall in a time interval

In the same interval of time ∆t, the total momentum transferred by the molecules

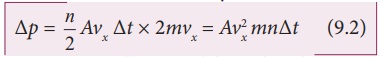
From Newton’s second law, the change in momentum in a small interval of time gives rise to force.

The force exerted by the molecules on the wall (in magnitude)

Pressure, P = force divided by the area of the wall

Since all the molecules are moving completely in random manner, they do not have same speed. So we can replace the term v_x² by the average x2  in equation (9.4)

Since the gas is assumed to move in random direction, it has no preferred direction of motion (the effect of gravity on the molecules is neglected). It implies that the molecule has same average speed in all the three direction. So, 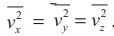 . The mean square speed is written as

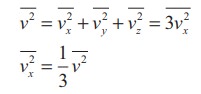
Using this in equation (9.5), we get

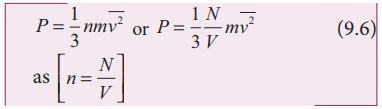
The following inference can be made from the above equation. The pressure exerted by the molecules depends on

(i) Number density n = N/V. It implies that if the number density increases then pressure will increase. For example when we pump air inside the cycle tyre or car tyre essentially the number density increases and as a result the pressure increases.

(ii) Mass of the molecule Since the pressure arises due to momentum transfer to the wall, larger mass will have larger momentum for a fixed speed. As a result the pressure will increase.

(iii) Mean square speed For a fixed mass if we increase the speed, the average speed will also increase. As a result the pressure will increase.

For simplicity the cubical container is taken into consideration. The above result is true for any shape of the container as the area A does not appear in the final expression (9.6). Hence the pressure exerted by gas molecules on the wall is independent of area of the wall.