Kinetic Theory of Gases | Physics - Mean Free Path | 11th Physics : UNIT 9 : Kinetic Theory of Gases
Chapter: 11th Physics : UNIT 9 : Kinetic Theory of Gases
Mean Free Path
MEAN
FREE PATH
Usually
the average speed of gas molecules is several hundred meters per second even at
room temperature. Odor from an open perfume bottle takes some time to reach us
even if we are closer to the room. The time delay is because the odor of the
molecules cannot travel straight to us as it undergoes a lot of collisions with
the nearby air molecules and moves in a zigzag path. This average distance travelled by the molecule between collisions is called
mean free path (λ). We can calculate
the mean free path based on kinetic theory.
Expression for mean free path
We know from postulates of kinetic theory that the molecules of a gas are in random motion and they collide with each other. Between two successive collisions, a molecule moves along a straight path with uniform velocity. This path is called mean free path.
Consider
a system of molecules each with diameter d. Let n be the number of molecules
per unit volume.
Assume
that only one molecule is in motion and all others are at rest as shown in the
Figure 9.8

If
a molecule moves with average speed v
in a time t, the distance travelled is vt.
In this time t, consider the molecule to move in an imaginary cylinder of
volume πd2vt. It collides with any molecule whose center is within this
cylinder. Therefore, the number of collisions is equal to the number of
molecules in the volume of the imaginary cylinder. It is equal to πd2vtn.
The total path length divided by the number of collisions in time t is the mean
free path.

Though
we have assumed that only one molecule is moving at a time and other molecules
are at rest, in actual practice all the molecules are in random motion. So the
average relative speed of one molecule with respect to other molecules has to
be taken into account. After some detailed calculations (you will learn in
higher classes) the correct expression for mean free path

The
equation (9.26) implies that the mean free path is inversely proportional to
number density. When the number density increases the molecular collisions
increases so it decreases the distance travelled by the molecule before
collisions.
Case1:
Rearranging the equation (9.26) using ‘m’ (mass of the molecule)
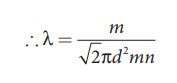
But
mn=mass per unit volume = ρ (density
of the gas)

The
equation (9.28) implies the following
1.
Mean free path increases with increasing temperature. As the temperature
increases, the average speed of each molecule will increase. It is the reason
why the smell of hot sizzling food reaches several meter away than smell of
cold food.
2.
Mean free path increases with decreasing pressure of the gas and diameter of
the gas molecules.
EXAMPLE 9.6
An
oxygen molecule is travelling in air at 300 K and 1 atm, and the diameter of
oxygen molecule is 1.2 × 10−10m.
Calculate the mean free path of oxygen molecule.
Solution
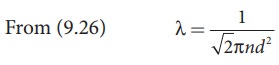
We
have to find the number density n By
using ideal gas law
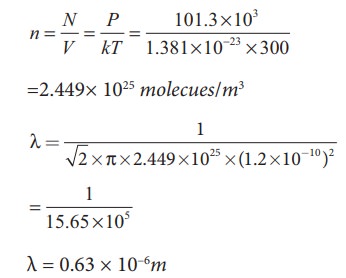
Related Topics