Physics - Magnetism and Magnetic Effects of Electric Current: Exercises and Example Solved Numerical problems | 12th Physics : Magnetism and Magnetic Effects of Electric Current
Chapter: 12th Physics : Magnetism and Magnetic Effects of Electric Current
Magnetism and Magnetic Effects of Electric Current: Exercises and Example Solved Numerical problems
Numerical problems
1. A bar magnet having a magnetic moment ![]() is cut into four pieces i.e., first cut in two pieces along the axis of the magnet and each piece is further cut into two pieces. Compute the magnetic moment of each piece.
is cut into four pieces i.e., first cut in two pieces along the axis of the magnet and each piece is further cut into two pieces. Compute the magnetic moment of each piece.

Answer: ![]() new = 1/4
new = 1/4![]()
2. A conductor of linear mass density 0.2 g m-1 suspended by two flexible wire as shown in figure. Suppose the tension in the supporting wires is zero when it is kept inside the magnetic field of 1 T whose direction is into the page. Compute the current inside the conductor and also the direction of the current. Assume g = 10 m s-2
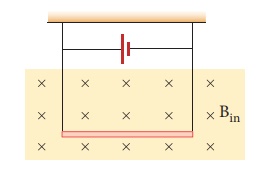

Answer: 2 mA
3. A circular coil with cross-sectional area 0.1 cm2 is kept in a uniform magnetic field of strength 0.2 T. If the current passing in the coil is 3 A and plane of the loop is perpendicular to the direction of magnetic field. Calculate
(a) total torque on the coil
(b) total force on the coil
(c) average force on each electron in the coil due to the magnetic field of the free electron density for the material of the wire is 1028 m-3.

Answer: (a) zero (b) zero (c) 0.6 x 10-23 N
4. A bar magnet is placed in a uniform magnetic field whose strength is 0.8 T. Suppose the bar magnet orient at an angle 30┬║ with the external field experiences a torque of 0.2 N m. Calculate:
(i) the magnetic moment of the magnet (ii) the work done by an applied force in
(ii) moving it from most stable configuration to the most unstable configuration and also compute the work done by the applied magnetic field in this case.

Answer: (i) 0.5 A m2 (ii) W = 0.8 J and Wmag = -0.8 J
5. A non - conducting sphere has a mass of 100ŌĆåg and radius 20ŌĆåcm. A flat compact coil of wire with turns 5 is wrapped tightly around it with each turns concentric with the sphere. This sphere is placed on an inclined plane such that plane of coil is parallel to the inclined plane. A uniform magnetic field of 0.5 T exists in the region in vertically upward direction. Compute the current I required to rest the sphere in equilibrium.
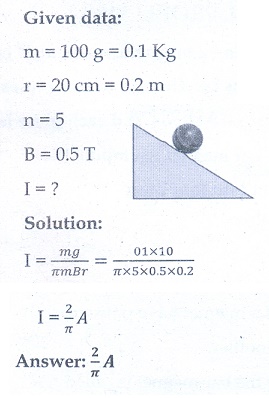
Answer: 2/ ŽĆ A
6. Calculate the magnetic field at the center of a square loop which carries a current of 1.5 A, length of each loop is 50 cm.

Answer: 3.4 x 10-6 T
7. Show that the magnetic field at any point on the axis of the solenoid having n turns per unit length is B = 1/2 ┬Ą nI(cos ╬Ė1 ŌłÆ cos ╬Ė2 ).
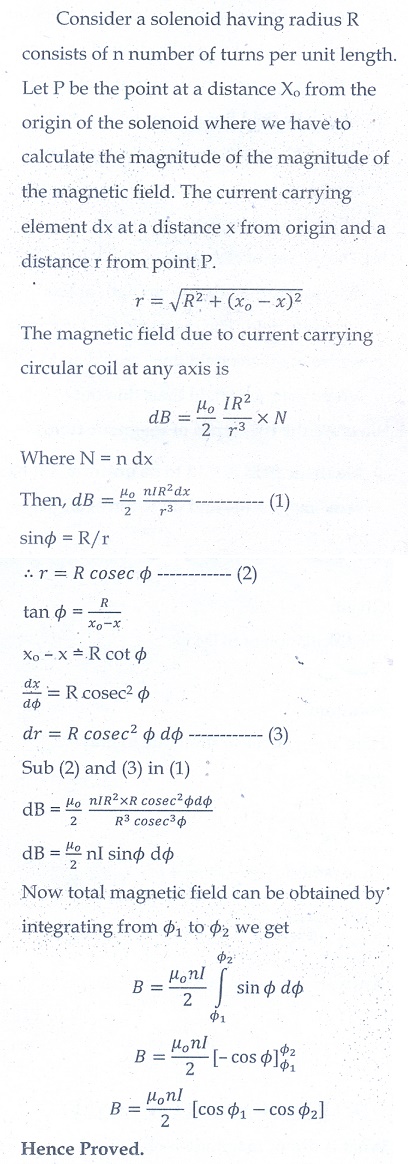
8. Let I1 and I2 be the steady currents passing through a long horizontal wire XY and PQ respectively. The wire PQ is fixed in horizontal plane and the wire XY be is allowed to move freely in a vertical plane. Let the wire XY is in equilibrium at a height d over the parallel wire PQ as shown in figure.
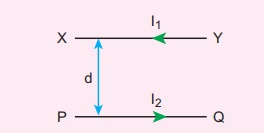
Show that if the wire XY is slightly displaced and released, it executes Simple Harmonic Motion (SHM). Also, compute the time period of oscillations.

Answer: ay = -Žē2y (SHM) and time period T = 2ŽĆ ŌłÜ[d/ g] in sec
EarthŌĆÖs magnetic field and magnetic elements: Solved Example Problems
EXAMPLE 3.1
The horizontal component and vertical components of EarthŌĆÖs magnetic field at a place are 0.15 G and 0.26 G respectively. Calculate the angle of dip and resultant magnetic field.
Solution:
BH = 0.15 G and BV = 0.26 G
tan I = 00.26/0.15 ŌćÆ I = tan ŌłÆ1(1. 732) =60┬║
The resultant magnetic field of the Earth is
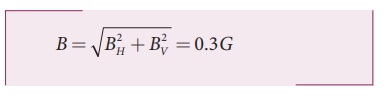
Basic properties of magnets: Solved Example Problems
EXAMPLE 3.2
Let the magnetic moment of a bar magnet be ![]() m whose magnetic length is d = 2l and pole strength is qm. Compute the magnetic moment of the bar magnet when it is cut into two pieces
m whose magnetic length is d = 2l and pole strength is qm. Compute the magnetic moment of the bar magnet when it is cut into two pieces
(a) along its length
(b) perpendicular to its length.
Solution
(a) a bar magnet cut into two pieces along its length:

When the bar magnet is cut along the axis into two pieces, new magnetic pole strength is qŌĆ▓m = qm/2 but magnetic length does not change. So, the magnetic moment is

In vector notation,
(b) a bar magnet cut into two pieces perpendicular to the axis:

When the bar magnet is cut perpendicular to the axis into two pieces, magnetic pole strength will not change but magnetic length will be halved. So the magnetic moment is

EXAMPLE 3.3
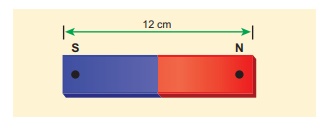
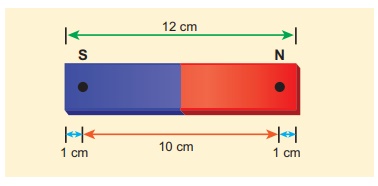
Compute the magnetic length of a uniform bar magnet if the geometrical length of the magnet is 12 cm. Mark the positions of magnetic pole points.
Solution
Geometrical length of the bar magnet is 12 cm
Magnetic length = 5/6 x (geometrical length)
= 5/6 x 12 = 10cm
In this figure, the dot implies the pole points.
EXAMPLE 3.4
Calculate the magnetic flux coming out from the surface containing magnetic dipole (say, a bar magnet) as shown in figure.
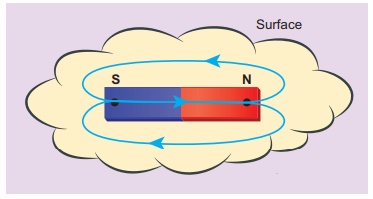
Solution
Magnetic dipole is kept, the total flux emanating from the closed surface S is zero. So,
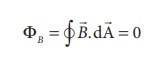
Here the integral is taken over closed surface. Since no isolated magnetic pole (called magnetic monopole) exists, this integral is always zero,
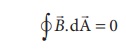
This is similar to GaussŌĆÖs law in electrostatics. (Refer unit 1)
CoulombŌĆÖs Inverse Square Law of Magnetism: Solved Example Problems
EXAMPLE 3.5
The repulsive force between two magnetic poles in air is 9 x 10-3 N. If the two poles are equal in strength and are separated by a distance of 10 cm, calculate the pole strength of each pole.
Solution:
The force between two poles are given by

The magnitude of the force is
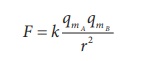
Given :ŌĆé F = 9 x 10-3N, r = 10 cm = 10 x 10-2 m
Therefore,
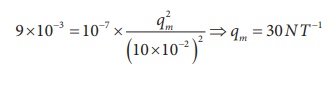
EXAMPLE 3.6
A short bar magnet has a magnetic moment of 0.5 J T-1. Calculate magnitude and direction of the magnetic field produced by the bar magnet which is kept at a distance of 0.1 m from the center of the bar magnet along (a) axial line of the bar magnet and (b) normal bisector of the bar magnet.
Solution
Given magnetic moment 0.5 J T-1 and distance r = 0.1 m
(a) When the point lies on the axial line of the bar magnet, the magnetic field for short magnet is given by
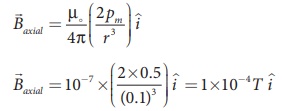
Hence, the magnitude of the magnetic field along axial is Baxial = 1 x 10-4 T and direction is towards South to North.
(b) When the point lies on the normal bisector (equatorial) line of the bar magnet, the magnetic field for short magnet is given by

Hence, the magnitude of the magnetic field along axial is Bequatorial = 0.5 x 10-4 T and direction is towards North to South.
Note that magnitude of Baxial is twice that of magnitude of Bequatorial and the direction of Baxial and Bequatorial are opposite.
Torque Acting on a Bar Magnet in Uniform Magnetic Field: Solved Example Problems
EXAMPLE 3.7
Show the time period of oscillation when a bar magnet is kept in a uniform magnetic field is 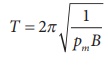 in second, where I represents moment Pm of inertia of the bar magnet, pm is the magnetic moment and is the magnetic field.
in second, where I represents moment Pm of inertia of the bar magnet, pm is the magnetic moment and is the magnetic field.
Solution
The magnitude of deflecting torque (the torque which makes the object rotate) acting on the bar magnet which will tend to align the bar magnet parallel to the direction of the uniform magnetic field ![]() is
is
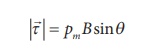
The magnitude of restoring torque acting on the bar magnet can be written as
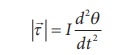
Under equilibrium conditions, both magnitude of deflecting torque and restoring torque will be equal but act in the opposite directions, which means
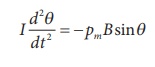
The negative sign implies that both are in opposite directions. The above equation can be written as

This is non-linear second order homogeneous differential equation. In order to make it linear, we use small angle approximation as we did in XI volume II (Unit 10 ŌĆō oscillations, Refer section 10.4.4) i.e., sin, we get
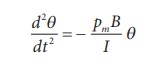
This linear second order homogeneous differential equation is a Simple Harmonic differential equation. Therefore,
Comparing with Simple Harmonic Motion (SHM) differential equation
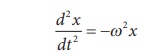
where Žē is the angular frequency of the oscillation.
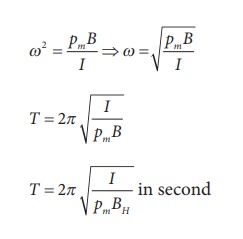
where, BH is the horizontal component of EarthŌĆÖs magnetic field.
Potential energy of a bar magnet in a uniform magnetic field: Solved Example Problems
EXAMPLE 3.8
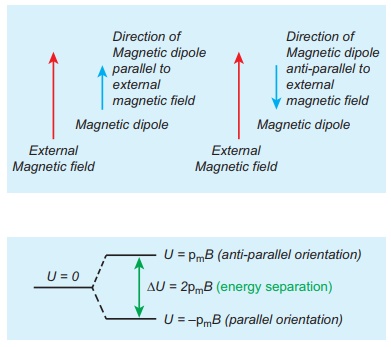
Consider a magnetic dipole which on switching ON external magnetic field orient only in two possible ways i.e., one along the direction of the magnetic field (parallel to the field) and another anti-parallel to magnetic field. Compute the energy for the possible orientation. Sketch the graph.
Solution
Let ![]() m be the dipole and before switching ON the external magnetic field, there is no orientation. Therefore, the energy U = 0.
m be the dipole and before switching ON the external magnetic field, there is no orientation. Therefore, the energy U = 0.
As soon as external magnetic field is switched ON, the magnetic dipole orient parallel (╬Ė = 0┬║) to the magnetic field with energy,
Uparallel = Uminimum = ŌłÆ pm B cos0
Uparallel = ŌłÆ pm B
since cos 0┬║ = 1
Otherwise, the magnetic dipole orients anti-parallel (╬Ė = 180┬║) to the magnetic field with energy,
UantiŌłÆ parallel = U maximum =ŌłÆ pmB cos180
ŌćÆU antiŌłÆparallel = pmB
since cos 180┬║ = -1
Tangent law and Tangent Galvanometer : Solved Example Problems
EXAMPLE 3.9
A coil of a tangent galvanometer of diametre 0.24 m has 100 turns. If the horizontal component of EarthŌĆÖs magnetic field is 25 ├Ś 10-6 T then, calculate the current which gives a deflection of 60┬║.
Solution
The diameter of the coil is 0.24 m.
Therefore, radius of the coil is 0.12 m.
Number of turns is 100 turns. EarthŌĆÖs magnetic field is 25 x 10-6 T
Deflection is
╬Ė=60 ┬║ Ō¤╣ tan 60 ┬║ = ŌłÜ3 = 1.732
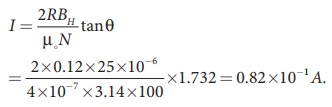
I = 0.082 A
Magnetic Properties: Solved Example Problems
EXAMPLE 3.10
Compute the intensity of magnetisation of the bar magnet whose mass, magnetic moment and density are 200 g, 2 A m2 and 8 g cm-3, respectively.
Solution
Density of the magnet is

EXAMPLE 3.11

EXAMPLE 3.12
Two materials X and Y are magnetised, whose intensity of magnetisation are 500 A m-1 and 2000 A m-1, respectively. If the magnetising field is 1000 A m-1, then which one among these materials can be easily magnetized?.
Solution
The susceptibility of material X is
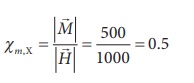
The susceptibility of material Y is
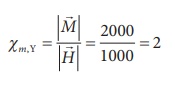
Since, susceptibility of material Y is greater than that of material X, material Y can be easily magnetized than X.
Hysteresis: Solved Example Problems
EXAMPLE 3.13
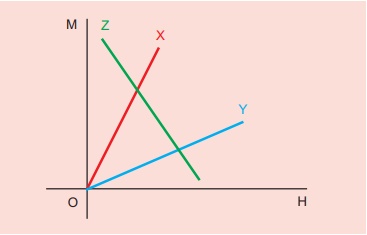
The following figure shows the variation of intensity of magnetisation with the applied magnetic field intensity for three magnetic materials X, Y and Z. Identify the materials X,Y and Z.
Solution
The slope of M-H graph measures the magnetic susceptibility, which is
Žćm = M / H
Material X: Slope is positive and larger value. So, it is a ferromagnetic material.
Material Y: Slope is positive and lesser value than X. So, it could be a paramagnetic material.
Material Z: Slope is negative and hence, it is a diamagnetic material.
MaxwellŌĆÖs right hand cork screw rule: Solved Example Problems
EXAMPLE 3.14
The magnetic field shown in the figure is due to the current carrying wire. In which direction does the current flow in the wire?.
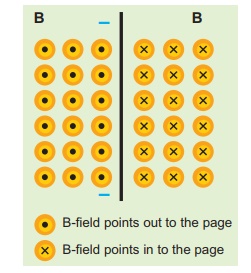
Solution
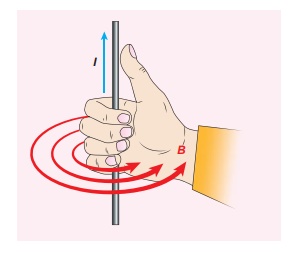
Using right hand rule, current flows upwards.
Magnetic field due to long straight conductor carrying current : Solved Example Problems
EXAMPLE 3.15
Calculate the magnetic field at a point P which is perpendicular bisector to current carrying straight wire as shown in figure.
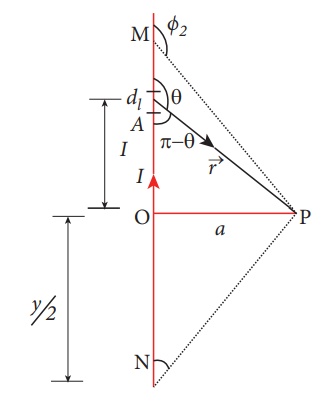
Solution
Let the length MN = y and the point P is on its perpendicular bisector. Let O be the point on the conductor as shown in figure.

The result obtained is same as we obtained in equation (3.39).
EXAMPLE 3.16
Show that for a straight conductor, the magnetic field
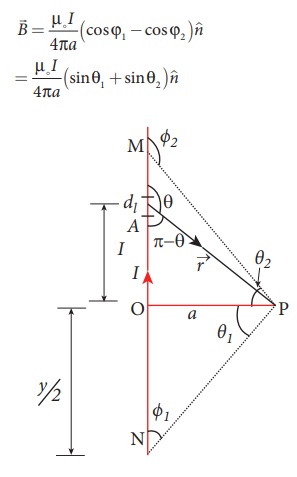
Solution:
In a right angle triangle OPN, let the angle ŌłĀ OPN = ╬Ė1 which implies, ŽĢ1 = ŽĆ /2 ŌłÆ ╬Ė1 and also in a right angle triangle OPM, ŌłĀOPM = ╬Ė2 which implies, ŽĢ2 = ŽĆ/2 + ╬Ė2
Hence,
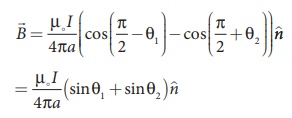
Magnetic field produced along the axis of the current carrying circular coil: Solved Example Problems
EXAMPLE 3.17
What is the magnetic field at the center of the loop shown in figure?
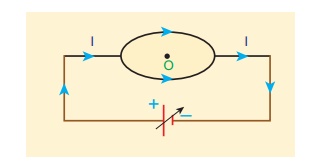
Solution
The magnetic field due to current in the upper hemisphere and lower hemisphere of the circular coil are equal in magnitude but opposite in direction. Hence, the net magnetic field at the center of the loop (at point O) is zero ![]() .
.
Magnetic field due to the current carrying wire of infinite length using Amp├©reŌĆÖs law : Solved Example Problems
EXAMPLE 3.18
Compute the magnitude of the magnetic field of a long, straight wire carrying a current of 1A at distance of 1m from it. Compare it with EarthŌĆÖs magnetic field.
Solution
Given that 1 = 1 A and radius r = 1 m

But the EarthŌĆÖs magnetic field is BEarth Ōēł 10ŌłÆ5 T
So, Bstraightwire is one hundred times smaller than BEarth.
Magnetic field due to a long current carrying solenoid: Solved Example Problems
EXAMPLE 3.19
Calculate the magnetic field inside a solenoid, when
(a) the length of the solenoid becomes twice and fixed number of turns
(b) both the length of the solenoid and number of turns are double
(c) the number of turns becomes twice for the fixed length of the solenoid
Compare the results.
Solution
The magnetic field of a solenoid (inside) is
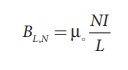
(a) length of the solenoid becomes twice and fixed number of turns
LŌåÆ2L (length becomes twice)
NŌåÆN (number of turns are fixed)
The magnetic field is
B2L , N = ┬Ą NI/2L = 1/2 BL ,N
(b) both the length of the solenoid and number of turns are double
LŌåÆ2L (length becomes twice)
NŌåÆ2N (number of turns becomes twice)
The magnetic field is

(c) the number of turns becomes twice but for the fixed length of the solenoid
LŌåÆL (length is fixed)
NŌåÆ2N (number of turns becomes twice)
The magnetic field is
BL ,2 N = ┬Ą, 2NI/L = 2BL ,N
From the above results,
BL ,2 N > B2 L ,2 N > B2 L , N
Thus, strength of the magnetic field is increased when we pack more loops into the same length for a given current.
Force on a moving charge in a magnetic field: Solved Example Problems
EXAMPLE 3.20
A particle of charge q moves with along positive y - direction invelocity ![]() a magnetic field
a magnetic field ![]() . Compute the Lorentz force experienced by the particle (a) when magnetic field is along positive y-direction (b) when magnetic field points in positive z - direction (c) when magnetic field is in zy - plane and making an angle ╬Ė with velocity of the particle. Mark the direction of magnetic force in each case.
. Compute the Lorentz force experienced by the particle (a) when magnetic field is along positive y-direction (b) when magnetic field points in positive z - direction (c) when magnetic field is in zy - plane and making an angle ╬Ė with velocity of the particle. Mark the direction of magnetic force in each case.
Solution
Velocity of the particle is 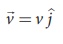
(a) Magnetic field is along positive y - direction, this implies, 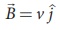

From Lorentz force, 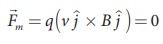
So, no force acts on the particle when it moves along the direction of magnetic field.
(b) Magnetic field points in positive z - direction, this implies, 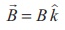

From Lorentz force,
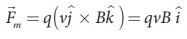
Therefore, the magnitude of the Lorentz force is qvB and direction is along positive x - direction.
(c) Magnetic field is in zy - plane and making an angle ╬Ė with the velocity of the particle, which implies 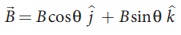
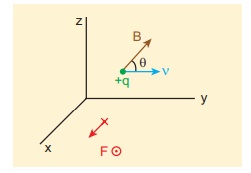
From Lorentz force,
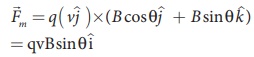
EXAMPLE 3.21
Compute the work done and power delivered by the Lorentz force on the particle of charge q moving with velocity ![]() . Calculate the angle between Lorentz force and velocity of the charged particle and also interpret the result.
. Calculate the angle between Lorentz force and velocity of the charged particle and also interpret the result.
Solution
For a charged particle moving on a magnetic field,
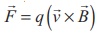
The work done by the magnetic field is

Since ![]() is perpendicular to
is perpendicular to ![]() and hence
and hence 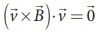 This means that Lorentz force do no work on the particle. From work kinetic energy theorem, (Refer section 4th chapter, XI th standard Volume I)
This means that Lorentz force do no work on the particle. From work kinetic energy theorem, (Refer section 4th chapter, XI th standard Volume I)
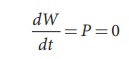
Since,  and
and ![]() are perpendicular to each other. The angle between Lorentz force and velocity of the charged particle is 90┬║. Thus Lorentz force changes the direction of the velocity but not the magnitude of the velocity. Hence Lorentz force does no work and also does not alter kinetic energy of the particle.
are perpendicular to each other. The angle between Lorentz force and velocity of the charged particle is 90┬║. Thus Lorentz force changes the direction of the velocity but not the magnitude of the velocity. Hence Lorentz force does no work and also does not alter kinetic energy of the particle.
Motion of a charged particle in a uniform magnetic field: Solved Example Problems
EXAMPLE 3.22
An electron moving perpendicular to a uniform magnetic field 0.500 T undergoes circular motion of radius 2.80 mm. What is the speed of electron?
Solution
Charge of an electron q = -1.60 ├Ś 10-19 C
Ō¤╣ |q| = 1.60 ├Ś10ŌłÆ19 C
Magnitude of magnetic field B = 0.500 T
Mass of the electron, m = 9.11 ├Ś 10-31 kg
Radius of the orbit, r = 2.50 mm = 2.50 ├Ś 10-3 m
Velocity of the electron, v = |q| rB/m
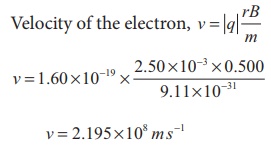
v = 2.195 ├Ś108 m sŌłÆ1
EXAMPLE 3.23
A proton moves in a uniform magnetic field of strength 0.500 T magnetic field is directed along the x-axis. At initial time, t = 0 s, the proton has velocity 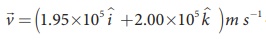 . Find
. Find
(a) At initial time, what is the acceleration of the proton.
(b) Is the path circular or helical?. If helical, calculate the radius of helical trajectory and also calculate the pitch of the helix (Note: Pitch of the helix is the distance travelled along the helix axis per revolution).
Solution

Pitch of the helix is the distance travelled along x-axis in a time T, which is P = vx T
But time,
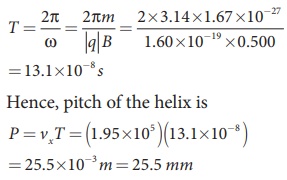
The proton experiences appreciable acceleration in the magnetic field, hence the pitch of the helix is almost six times greater than the radius of the helix.
EXAMPLE 3.24
Two singly ionized isotopes of uranium 23592U and 23892U (isotopes have same atomic number but different mass number) are sent with velocity 1.00 ├Ś 105 m s-1 into a magnetic field of strength 0.500 T normally. Compute the distance between the two isotopes after they complete a semi-circle. Also compute the time taken by each isotope to complete one semi-circular path. (Given: masses of the isotopes: m235 = 3.90 x 10-25 kg and m238 = 3.95 x 10-25 kg)
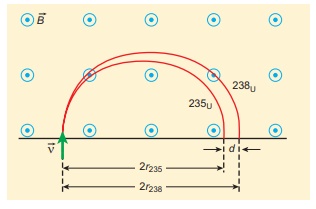
Solution
Since isotopes are singly ionized, they have equal charge which is equal to the charge of an electron, q = - 1.6 ├Ś 10-19 C. Mass of uranium 23592U and 23892U are 3.90 ├Ś 10-25 kg and 3.95 ├Ś 10-25 kg respectively. Magnetic field applied, B = 0.500 T. Velocity of the electron is 1.00 ├Ś 105 m s-1, then
(a) the radius of the path of 23592U is r235

The diameter of the semi-circle due to 23892U is d238 = 2r238 = 98.8 cm
Therefore the separation distance between the isotopes is ╬öd = d238 ŌłÆ d235 = 1.2cm
(b) The time taken by each isotope to complete one semi-circular path are

Note that even though the difference between mass of two isotopes are very small, this arrangement helps us to convert this small difference into an easily measurable distance of separation. This arrangement is known as mass spectrometer. A mass spectrometer is used in many areas in sciences, especially in medicine, in space science, in geology etc. For example, in medicine, anaesthesiologists use it to measure the respiratory gases and biologist use it to determine the reaction mechanisms in photosynthesis.
Motion of a charged particle under crossed electric and magnetic field (velocity selector): Solved Example Problems
EXAMPLE 3.25
Let E be the electric field of magnitude 6.0 ├Ś 106 N C-1 and B be the magnetic field magnitude 0.83 T. Suppose an electron is accelerated with a potential of 200 V, will it show zero deflection?. If not, at what potential will it show zero deflection.
Solution:
Electric field, E = 6.0 ├Ś 106 N C-1 and magnetic field, B = 0.83 T.
Then

When an electron goes with this velocity, it shows null deflection. Since the accelerating potential is 200 V, the electron acquires kinetic energy because of this accelerating potential. Hence,
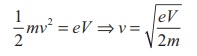
Since the mass of the electron, m = 9 .1├Ś10ŌłÆ31 kg and charge of an electron, |q| = e = 1.6 ├Ś10ŌłÆ19 C. The velocity due to accelerating potential 200 V
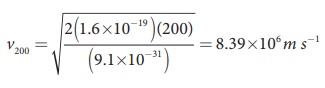
Since the speed v200 > v, the electron is deflected towards direction of Lorentz force. So, in order to have null deflection, the potential, we have to supply is

V =148 65 V
Cyclotron: Solved Example Problems
EXAMPLE 3.26
Suppose a cyclotron is operated to accelerate protons with a magnetic field of strength 1 T. Calculate the frequency in which the electric field between two Dees could be reversed.
Solution
Magnetic field B = 1 T
Mass of the proton, mp = 1.67 ├Ś10ŌłÆ27 kg
Charge of the proton, q = 1.60 ├Ś10ŌłÆ19 C
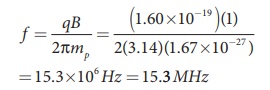
Force on a current carrying conductor placed in a magnetic field: Solved Example Problems
EXAMPLE 3.27
A metallic rod of linear density is 0.25 kg m-1 is lying horizontally on a smooth inclined plane which makes an angle of 45┬║ with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of strength 0.25 T is acting on it in the vertical direction. Calculate the electric current flowing in the rod to keep it stationary.
Solution
The linear density of the rod i.e., mass per unit length of the rod is 0.25 kg m-1
ŌćÆ m/l = 0.25 kg mŌłÆ1
Let I be the current flowing in the metallic rod. The direction of electric current is into the paper. The direction of magnetic force IBl is given by FlemingŌĆÖs left hand rule.
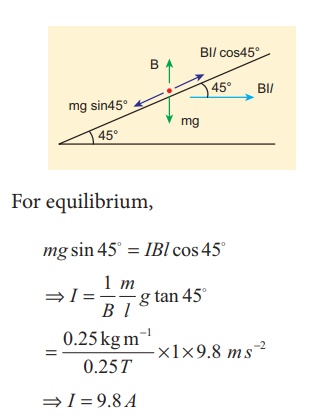
For equilibrium,
mg sin 45┬║ = IBl cos 45 ┬║
ŌćÆ I = I/B m/l g tan 45 ┬║
ŌćÆ I = 9.8 A
So, we need to supply current of 9.8 A to keep the metallic rod stationary.
Expression for to
rque on a current loop placed in a magnetic field: Solved Example Problems
EXAMPLE 3.28
Consider a circular wire loop of radius R, mass m kept at rest on a rough surface. Let I be the current flowing through the loop and ![]() be the magnetic field acting along horizontal as shown in Figure. Estimate the current I that should be applied so that one edge of the loop is lifted off the surface?
be the magnetic field acting along horizontal as shown in Figure. Estimate the current I that should be applied so that one edge of the loop is lifted off the surface?
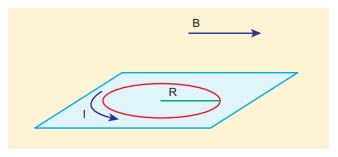
Solution

When the current is passed through the loop, the torque is produced. If the torque acting on the loop is increased then the loop will start to rotate. The loop will start to lift if and only if the magnitude of magnetic torque due to current applied equals to the gravitational torque as shown in Figure

The current estimated using this equation should be applied so that one edge of loop is lifted of the surface.
Moving coil galvanometer: Solved Example Problems
EXAMPLE 3.29
The coil of a moving coil galvanometer has 5 turns and each turn has an effective area of 2 ├Ś 10-2 m2. It is suspended in a magnetic field whose strength is 4 ├Ś 10-2 Wb m-2. If the torsional constant K of the suspension fibre is 4 ├Ś 10-9 N m deg-1.
(a) Find its current sensitivity in degree per micro - ampere.
(b) Calculate the voltage sensitivity of the galvanometer for it to have full scale deflection of 50 divisions for 25 mV.
(c) Compute the resistance of the galvanometer.
Solution
The number of turns of the coil is 5 turns
The area of each coil is 2 ├Ś 10-2 m2
Strength of the magnetic field is 4 ├Ś 10-2 Wb m-2
Torsional constant is 4 ├Ś 10-9 N m deg-1

EXAMPLE 3.30
The resistance of a moving coil galvanometer is made twice its original value in order to increase current sensitivity by 50%. Will the voltage sensitivity change? If so, by how much?.
Solution
Yes, voltage sensitivity will change.
Voltage sensitivity is Vs = Is/R
When the resistance is doubled, then new resistance is R ŌĆ▓ = 2R
Increase in current sensitivity is

Hence the voltage sensitivity decreases. The percentage decrease in voltage sensitivity is
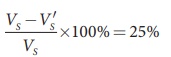
Related Topics