Chapter: 12th Physics : Magnetism and Magnetic Effects of Electric Current
Torque Acting on a Bar Magnet in Uniform Magnetic Field: Solved Example Problems
Torque Acting on a Bar Magnet in Uniform Magnetic Field: Solved Example Problems
EXAMPLE 3.7
Show the time period of oscillation when a bar magnet is kept in a uniform magnetic field is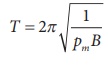 
in second, where I represents moment Pm of inertia of the bar magnet, pm is the magnetic moment and is the magnetic field.
Solution
The magnitude of deflecting torque (the torque which makes the object rotate) acting on the bar magnet which will tend to align the bar magnet parallel to the direction of the uniform magnetic field 
is
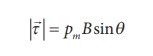
The magnitude of restoring torque acting on the bar magnet can be written as
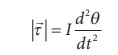
Under equilibrium conditions, both magnitude of deflecting torque and restoring torque will be equal but act in the opposite directions, which means
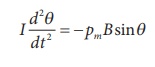
The negative sign implies that both are in opposite directions. The above equation can be written as
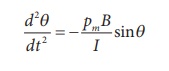
This is non-linear second order homogeneous differential equation. In order to make it linear, we use small angle approximation as we did in XI volume II (Unit 10 – oscillations, Refer section 10.4.4) i.e., sin, we get
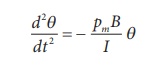
This linear second order homogeneous differential equation is a Simple Harmonic differential equation. Therefore,
Comparing with Simple Harmonic Motion (SHM) differential equation
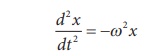
where ω is the angular frequency of the oscillation.
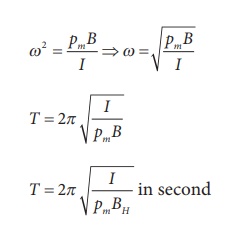
where, BH is the horizontal component of Earth’s magnetic field.
Potential energy of a bar magnet in a uniform magnetic field: Solved Example Problems
EXAMPLE 3.8
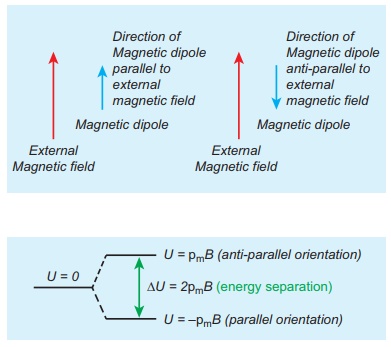
Consider a magnetic dipole which on switching ON external magnetic field orient only in two possible ways i.e., one along the direction of the magnetic field (parallel to the field) and another anti-parallel to magnetic field. Compute the energy for the possible orientation. Sketch the graph.
Solution
Let 
m be the dipole and before switching ON the external magnetic field, there is no orientation. Therefore, the energy U = 0.
As soon as external magnetic field is switched ON, the magnetic dipole orient parallel (θ = 0º) to the magnetic field with energy,
Uparallel = Uminimum = − pm B cos0
Uparallel = − pm B
since cos 0º = 1
Otherwise, the magnetic dipole orients anti-parallel (θ = 180º) to the magnetic field with energy,
Uanti− parallel = U maximum =− pmB cos180
⇒U anti−parallel = pmB
since cos 180º = -1
Tangent law and Tangent Galvanometer : Solved Example Problems
EXAMPLE 3.9
A coil of a tangent galvanometer of diametre 0.24 m has 100 turns. If the horizontal component of Earth’s magnetic field is 25 × 10-6 T then, calculate the current which gives a deflection of 60º.
Solution
The diameter of the coil is 0.24 m.
Therefore, radius of the coil is 0.12 m.
Number of turns is 100 turns. Earth’s magnetic field is 25 x 10-6 T
Deflection is
θ=60 º ⟹ tan 60 º = √3 = 1.732
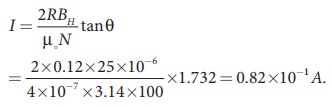
I = 0.082 A
Related Topics