Lorentz Force | Physics - Force on a current carrying conductor placed in a magnetic field | 12th Physics : Magnetism and Magnetic Effects of Electric Current
Chapter: 12th Physics : Magnetism and Magnetic Effects of Electric Current
Force on a current carrying conductor placed in a magnetic field
Force on a current carrying conductor placed in a magnetic field
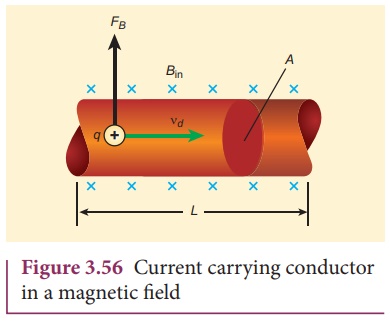
When a current carrying conductor is placed in a magnetic field, the force experienced by the wire is equal to the sum of Lorentz forces on the individual charge carriers in the wire. Consider a small segment of wire of length dl, with cross-sectional area A and current I as shown in Figure 3.56. The free electrons drift opposite to the direction of current. So the relation between current I and magnitude of drift velocity vd (Refer Unit 2) is

If the wire is kept in a magnetic field ![]() , then average force experienced by the charge (here, electron) in the wire is
, then average force experienced by the charge (here, electron) in the wire is

Let n be the number of free electrons per unit volume, therefore
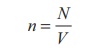
where N is the number of free electrons in the small element of volume V = A dl.
Hence Lorentz force on the wire of length dl is the product of the number of the electrons
(N = nA dl) and the force acting on an electron.
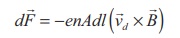
The length dl is along the length of the wire and hence the current element in the wire is 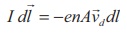
Therefore the force on the wire is
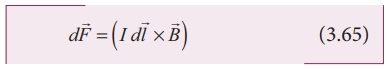
The force in a straight current carrying conducting wire of length l placed in a uniform magnetic field is

In magnitude,
F = BIl sin╬Ė
(a) If the conductor is placed along the direction of the magnetic field, the angle between them is ╬Ė = 0┬║. Hence, the force experienced by the conductor is zero.
(b) If the conductor is placed perpendicular to the magnetic field, the angle between them is ╬Ė =90┬║ Hence, the force experienced by the conductor is maximum, which is F = BIl.
FlemingŌĆÖs left hand rule (mnemonic)
When a current carrying conductor is placed in a magnetic field, the direction of the force experienced by it is given by FlemingŌĆÖs Left Hand Rule (FLHR) as shown in Figure 3.57.
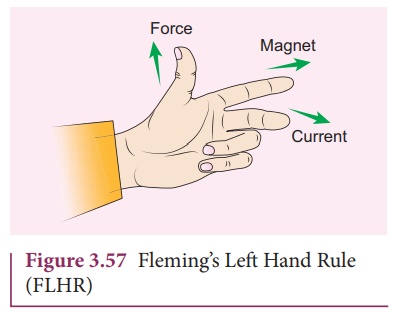
Stretch forefinger, the middle finger and the thumb of the left hand such that they are in mutually perpendicular directions. If forefinger points the direction of magnetic field, the middle finger points the direction of the electric current, then thumb will point the direction of the force experienced by the conductor.
EXAMPLE 3.27
A metallic rod of linear density is 0.25 kg m-1 is lying horizontally on a smooth inclined plane which makes an angle of 45┬║ with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of strength 0.25 T is acting on it in the vertical direction. Calculate the electric current flowing in the rod to keep it stationary.
Solution
The linear density of the rod i.e., mass per unit length of the rod is 0.25 kg m-1
ŌćÆ m/l = 0.25 kg mŌłÆ1
Let I be the current flowing in the metallic rod. The direction of electric current is into the paper. The direction of magnetic force IBl is given by FlemingŌĆÖs left hand rule.
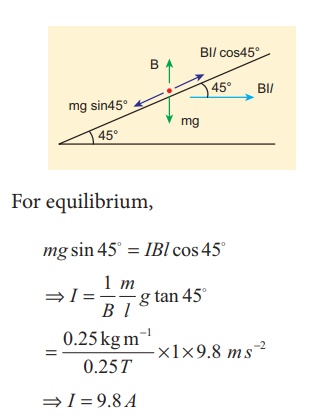
For equilibrium,
mg sin 45┬║ = IBl cos 45 ┬║
ŌćÆ I = I/B m/l g tan 45 ┬║
ŌćÆ I = 9.8 A
So, we need to supply current of 9.8 A to keep the metallic rod stationary.
Related Topics