Chapter: 12th Physics : Magnetism and Magnetic Effects of Electric Current
Potential energy of a bar magnet in a uniform magnetic field
Potential energy of a bar magnet in a uniform magnetic field
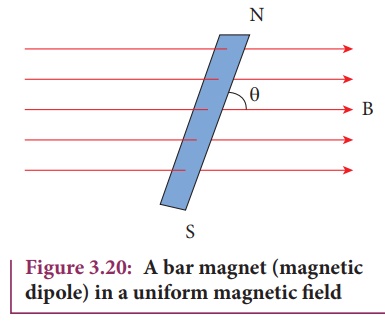
When a bar magnet (magnetic dipole) of dipole moment ![]() m is held at an angle ╬Ė with the direction of a uniform magnetic field
m is held at an angle ╬Ė with the direction of a uniform magnetic field ![]() , as shown in Figure 3.20 the magnitude of the torque acting on the dipole is
, as shown in Figure 3.20 the magnitude of the torque acting on the dipole is

If the dipole is rotated through a very small angular displacement d╬Ė against the torque ŽäB at constant angular velocity, then the work done by external torque (![]() ) for this small angular displacement is given by
) for this small angular displacement is given by

The bar magnet has to be moved at constant angular velocity, which implies that

Total work done in rotating the dipole from ╬Ė═┤ to ╬Ė is
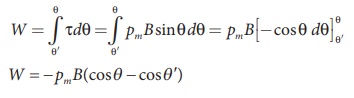
This work done is stored as potential energy in bar magnet at an angle ╬Ė when it is rotated from ╬Ė═┤ to ╬Ė and it can be written as

In fact, the equation (3.26) gives the difference in potential energy between the angular positions ╬Ė═┤ and ╬Ė. We can choose the reference point ╬Ė═┤ = 90o, so that second term in the equation becomes zero and the equation (3.26) can be written as

The potential energy stored in a bar magnet in a uniform magnetic field is given by

Case 1
(i) If ╬Ė = 0┬║, then
U = ŌłÆ pm B (cos0 ┬║ ) = ŌłÆ pm B
(ii) If ╬Ė = 180 ┬║, then
U= ŌłÆ pm B (cos180 ┬║) = pm B
We can infer from the above two results, the potential energy of the bar magnet is minimum when it is aligned along the external magnetic field and maximum when the bar magnet is aligned anti-parallel to external magnetic field.
EXAMPLE 3.8
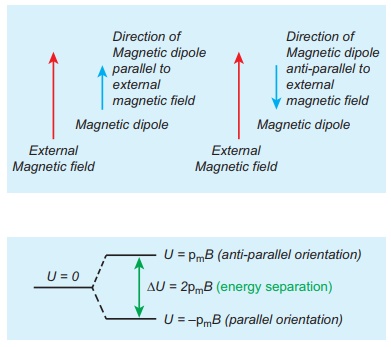
Consider a magnetic dipole which on switching ON external magnetic field orient only in two possible ways i.e., one along the direction of the magnetic field (parallel to the field) and another anti-parallel to magnetic field. Compute the energy for the possible orientation. Sketch the graph.
Solution
Let ![]() m be the dipole and before switching ON the external magnetic field, there is no orientation. Therefore, the energy U = 0.
m be the dipole and before switching ON the external magnetic field, there is no orientation. Therefore, the energy U = 0.
As soon as external magnetic field is switched ON, the magnetic dipole orient parallel (╬Ė = 0┬║) to the magnetic field with energy,
Uparallel = Uminimum = ŌłÆ pm B cos0
Uparallel = ŌłÆ pm B
since cos 0┬║ = 1
Otherwise, the magnetic dipole orients anti-parallel (╬Ė = 180┬║) to the magnetic field with energy,
UantiŌłÆ parallel = U maximum =ŌłÆ pmB cos180
ŌćÆU antiŌłÆparallel = pmB
since cos 180┬║ = -1
Related Topics