Current loop as a magnetic dipole

Current loop as a magnetic dipole

The magnetic field from the centre of a circular loop of radius R along the axis is given by

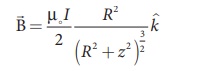
At larger distance Z >> R, therefore R2 + Z2  â‰ˆ Z2 , we have

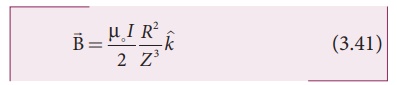
Let A be the area of the circular loop A = π R2. So rewriting the equation (3.41) in terms of area of the loop, we have

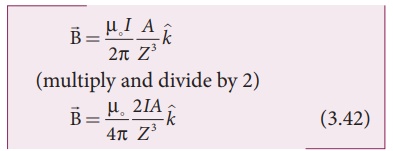
Comparing equation (3.42)   with equation (3.14) dimensionally, we get

pm = I A

where pm is called magnetic dipole moment. In vector notation,

This implies that a current carrying circular loop behaves as a magnetic dipole of magnetic moment m . So, the magnetic dipole moment of any current loop is equal to the product of the current and area of the loop.

Right hand thumb rule

In order to determine the direction of magnetic moment, we use right hand thumb rule (mnemonic) which states that

If we curl the fingers of right hand in the direction of current in the loop, then the stretched thumb gives the direction of the magnetic moment associated with the loop.