Expression for torque on a current loop placed in a magnetic field

TORQUE ON A CURRENT LOOP

The force on a current carrying wire in a magnetic field is responsible for the motor operation.

Expression for torque on a current loop placed in a magnetic field

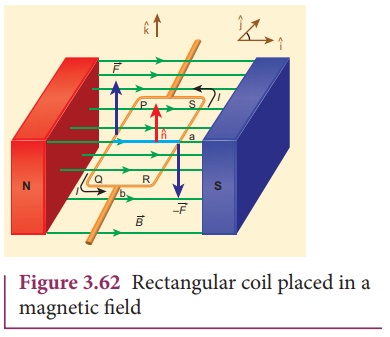
Consider a single rectangular loop PQRS kept in a uniform magnetic field . Let a and b be the length and breadth of the rectangular loop respectively. Let n ^  be the unit vector normal to the plane of the current loop. This unit vector n ^ completely describes the orientation of the loop. Let  be directed from north pole to south pole of the magnet as shown in Figure 3.62.

When an electric current is sent through the loop, the net force acting is zero but there will be net torque acting on it. For the sake of understanding, we shall consider two configurations of the loop; (i) unit vector n pointing perpendicular to the field (ii) unit vector pointing at an angle θ with the field.

(i) when unit vector n is perpendicular to the field

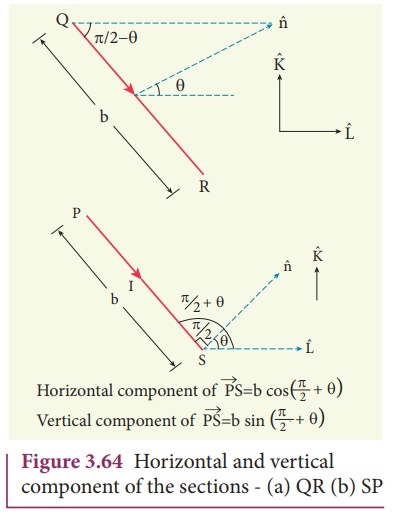
In the simple configuration, the unit vector n ^ is perpendicular to the field and plane of the loop is lying on xy plane as shown in Figure 3.62. Let the loop be divided into four sections PQ, QR, RS and SP. The Lorentz force on each loop can be calculated as follows:

Since, the unit vector normal to the plane is along the direction of -k^.

(d) The force on section SP

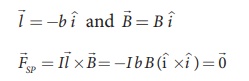
The net force on the rectangular loop is

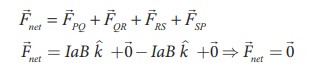
Hence, the net force on the rectangular loop in this configuration is zero. Now let us calculate the net torque due to these forces about an axis passing through the center

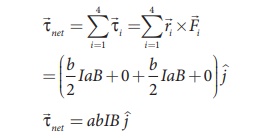
Since, A = ab is the area of the rectangular loop PQRS, the net torque for this configuration is

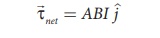
When the loop starts rotating due to this torque, the magnetic field  is no longer in the plane of the loop. So the above equation is the special case.

When the loop starts rotating about z axis due to this torque, the magnetic field  is no longer in the plane of the loop. So the above equation is the special case.

(ii) when unit vector n is at an angle θ with the field

In the general case, the unit normal vector n ^ and magnetic field  is with an angle θ as shown in Figure 3.63.

(a) The force on section PQ

Since, the unit vector normal to the plane n ^ is along the direction of k ^.

(b) The force on section QR

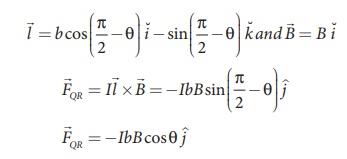
(c) The force on section RS

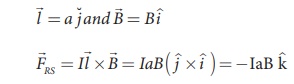
Since, the unit vector normal to the plane is along the direction of -k^.

(d) The force on section SP

The net force on the rectangular loop is

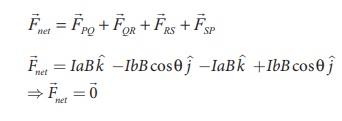
Hence, the net force on the rectangular loop in this configuration is also zero. Notice that the force on section QR and SP are not zero here. But, they have equal and opposite effects, but we assume the loop to be rigid, so no deformation. Hence, no torque produced by these two sections.

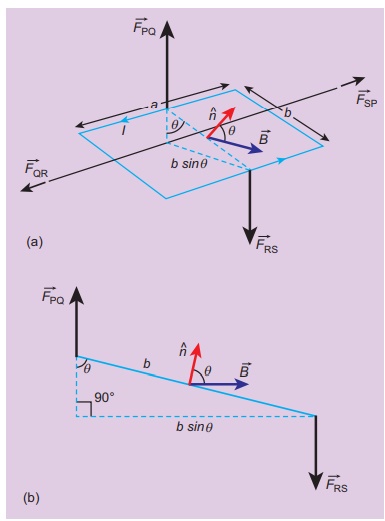
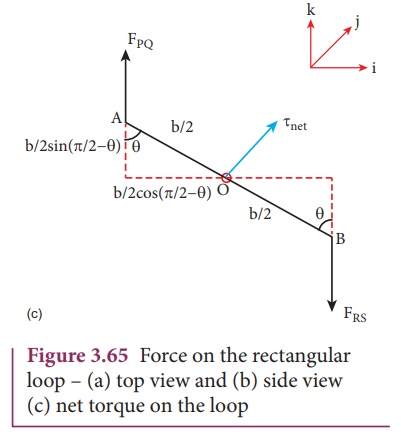
Even though the forces PQ and RS also are also equal and opposite, they are not collinear. So these two forces constitute a couple as shown in Figure 3.65 (a). Hence the net torque produced by these two forces about the axis of the rectangular loop is given by

Note that the net torque is in the positive y direction which tends to rotate the loop in clockwise direction about the y axis. If the current is passed in the other way (P→S→R→Q→P), then total torque will point in the negative y direction which tends to rotate the loop in anticlockwise direction about y axis.

Another important point is to note that the torque is less in this case compared to earlier case (where the n^ is perpendicular to the magnetic field ). It is because the perpendicular distance is reduced between the forces _PQ and _RS in this case.

The equation (3.68) can also be rewritten in terms of magnetic dipole moment

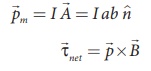
This is analogous expression for torque experienced by electric dipole in the uniform electric field

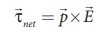  which is given in the Unit 1. (Section 1.4.3)

Cases:

(a) When θ = 90º, then the torque on the current loop is maximum which is

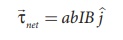
Note here m  points perpendicular to the magnetic field . The torque is maximum in this orientation.

(b) When θ = 0º or 180 º then the torque on the current loop is

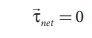
when θ = 0º m   is parallel to  and for θ = 180º m   , is anti - parallel to . The torque is zero in these orientations.

EXAMPLE 3.28

Consider a circular wire loop of radius R, mass m kept at rest on a rough surface. Let I be the current flowing through the loop and  be the magnetic field acting along horizontal as shown in Figure. Estimate the current I that should be applied so that one edge of the loop is lifted off the surface?

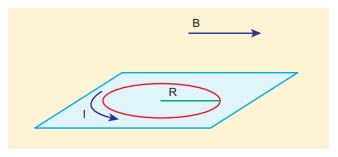
Solution

When the current is passed through the loop, the torque is produced. If the torque acting on the loop is increased then the loop will start to rotate. The loop will start to lift if and only if the magnitude of magnetic torque due to current applied equals to the gravitational torque as shown in Figure

The current estimated using this equation should be applied so that one edge of loop is lifted of the surface.