Physics - Basic properties of magnets | 12th Physics : Magnetism and Magnetic Effects of Electric Current
Chapter: 12th Physics : Magnetism and Magnetic Effects of Electric Current
Basic properties of magnets
Basic properties of magnets
Some basic terminologies and properties used in describing bar magnet.
(a) Magnetic dipole moment
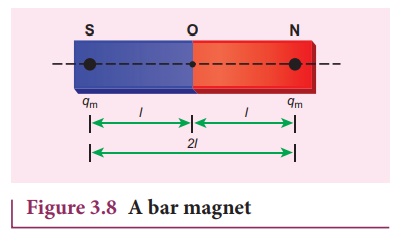
Consider a bar magnet as shown in Figure 3.8. Let qm be the pole strength (it is also called as magnetic charge) of the magnetic pole and let l be the distance between the geometrical center of bar magnet O and one end of the pole. The magnetic dipole moment is defined as the product of its pole strength and magnetic length. It is a vector quantity, denoted by ![]() m.
m.

where ![]() is the vector drawn from south pole to north pole and its magnitude |
is the vector drawn from south pole to north pole and its magnitude |![]() |2l .
|2l .
The magnitude of magnetic dipole moment is pm = 2qm l
The SI unit of magnetic moment is A m2. Note that the direction of magnetic moment is from South pole to North pole.
(b) Magnetic field
Magnetic field is the region or space around every magnet within which its influence can be felt by keeping another magnet in that region. The magnetic field ![]() at a point is defined as a force experienced by the bar magnet of unit pole strength.
at a point is defined as a force experienced by the bar magnet of unit pole strength.

Its unit is N A-1 m-1.
(c) Types of magnets
Magnets are classified into natural magnets and artificial magnets. For example, iron, cobalt, nickel, etc. are natural magnets. Strengths of natural magnets are very weak and the shapes of the magnet are irregular. Artificial magnets are made by us in order to have desired shape and strength. If the magnet is in the form of rectangular shape or cylindrical shape, then it is known as bar magnet.
Properties of magnet
The following are the properties of bar magnet (Figure 3.9)
1. A freely suspended bar magnet will always point along the north-south direction.
2. A magnet attracts another magnet or magnetic substances towards itself. The attractive force is maximum near the end of the bar magnet. When a bar magnet is dipped into iron filling, they cling to the ends of the magnet.
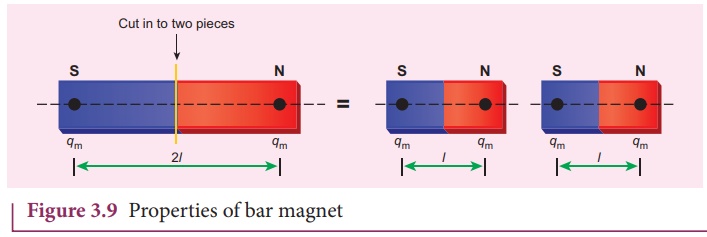
3. When a magnet is broken into pieces, each piece behaves like a magnet with poles at its ends.
4. Two poles of a magnet have pole strength equal to one another.
5. The length of the bar magnet is called geometrical length and the length between two magnetic poles in a bar magnet is called magnetic length. Magnetic length is always slightly smaller than geometrical length. The ratio of magnetic length and geometrical length is 5/6 .
Magnetic length / Geometricallength = 5/6 = 0.833
EXAMPLE 3.2
Let the magnetic moment of a bar magnet be ![]() m whose magnetic length is d = 2l and pole strength is qm. Compute the magnetic moment of the bar magnet when it is cut into two pieces
m whose magnetic length is d = 2l and pole strength is qm. Compute the magnetic moment of the bar magnet when it is cut into two pieces
(a) along its length
(b) perpendicular to its length.
Solution
(a) a bar magnet cut into two pieces along its length:
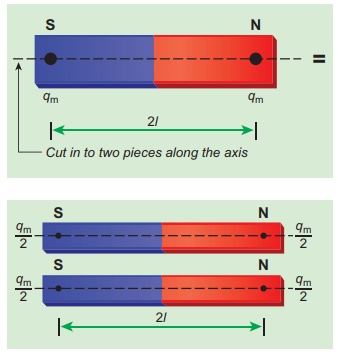
When the bar magnet is cut along the axis into two pieces, new magnetic pole strength is q′m = qm/2 but magnetic length does not change. So, the magnetic moment is

In vector notation,
(b) a bar magnet cut into two pieces perpendicular to the axis:
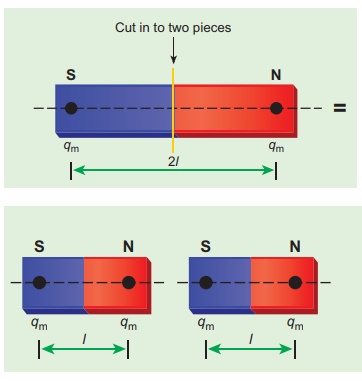
When the bar magnet is cut perpendicular to the axis into two pieces, magnetic pole strength will not change but magnetic length will be halved. So the magnetic moment is

EXAMPLE 3.3
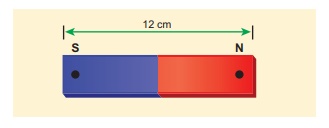
Compute the magnetic length of a uniform bar magnet if the geometrical length of the magnet is 12 cm. Mark the positions of magnetic pole points.
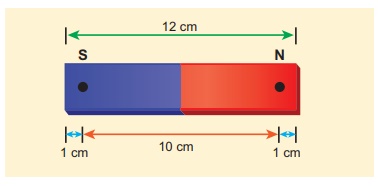
Solution
Geometrical length of the bar magnet is 12 cm
Magnetic length = 5/6 x (geometrical length)
= 5/6 x 12 = 10cm
In this figure, the dot implies the pole points.
Magnetic field lines
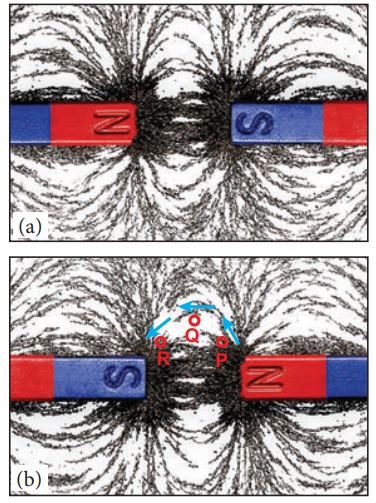
1. Magnetic field lines are continuous closed curves. The direction of magnetic field lines is from North pole to South pole outside the magnet (Figure 3.10) and South pole to North pole inside the magnet.
2. The direction of magnetic field at any point on the curve is known by drawing tangent to the magnetic line of force at that point. In the Figure No. 3.10 (b), the tangent drawn at points P, Q and R gives the direction of magnetic field B at that point.
3. Magnetic field lines never intersect each other. Otherwise, the magnetic compass needle would point towards two directions, which is not possible.
4. The degree of closeness of the field lines determines the relative strength of the magnetic field. The magnetic field is strong where magnetic field lines crowd and weak where magnetic field lines thin out.
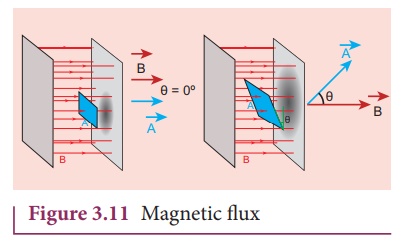
(d) Magnetic flux
The number of magnetic field lines crossing per unit area is called magnetic flux ΦB. Mathematically, the magnetic flux through a surface of area A in a uniform magnetic field is defined as
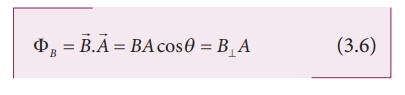

where θ is the angle between B and A as shown in Figure 3.11.
Special cases
When ![]() is normal to the surface i.e., θ = 0º, the magnetic flux is ΦB = BA (maximum).
is normal to the surface i.e., θ = 0º, the magnetic flux is ΦB = BA (maximum).
When ![]() is parallel to the surface i.e., θ = 90º, the magnetic flux is ΦB = 0.
is parallel to the surface i.e., θ = 90º, the magnetic flux is ΦB = 0.
Suppose the magnetic field is not uniform over the surface, the equation (3.6) can be written as
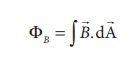
Magnetic flux is a scalar quantity. The SI unit for magnetic flux is weber, which is denoted by symbol Wb. Dimensional formula for magnetic flux is ML2T -2 A-1 . The CGS unit of magnetic flux is Maxwell.
1 weber = 108 maxwell
The magnetic flux density can also be defined as the number of magnetic field lines crossing unit area kept normal to the direction of line of force. Its unit is Wb m-2 or tesla.
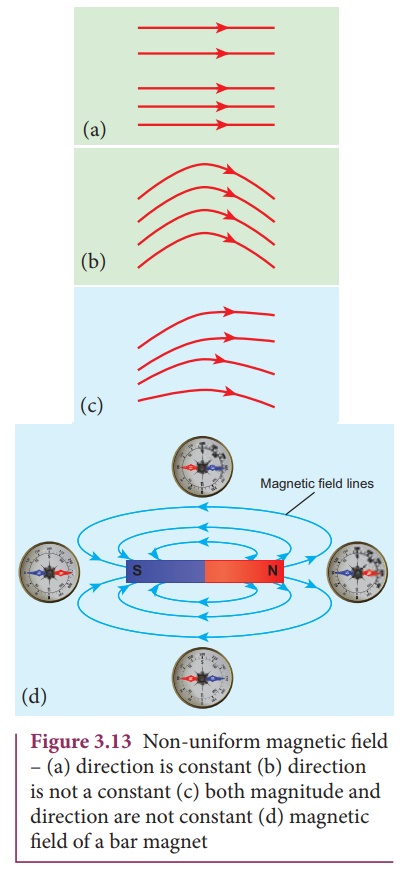
(e) Uniform magnetic field and Non-uniform magnetic field
Uniform magnetic field

Magnetic field is said to be uniform if it has same magnitude and direction at all the points in a given region. Example, locally Earth’s magnetic field is uniform.
The magnetic field of Earth has same value over the entire area of your school!
Non-uniform magnetic field
Magnetic field is said to be non-uniform if the magnitude or direction or both varies at all its points. Example: magnetic field of a bar magnet
EXAMPLE 3.4
Calculate the magnetic flux coming out from the surface containing magnetic dipole (say, a bar magnet) as shown in figure.
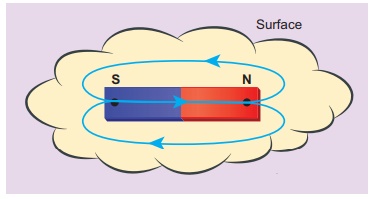
Solution
Magnetic dipole is kept, the total flux emanating from the closed surface S is zero. So,
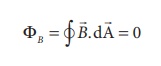
Here the integral is taken over closed surface. Since no isolated magnetic pole (called magnetic monopole) exists, this integral is always zero,
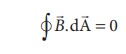
This is similar to Gauss’s law in electrostatics. (Refer unit 1)
Related Topics