Biot - Savart Law | Physics - Magnetic field due to long straight conductor carrying current | 12th Physics : Magnetism and Magnetic Effects of Electric Current
Chapter: 12th Physics : Magnetism and Magnetic Effects of Electric Current
Magnetic field due to long straight conductor carrying current
Magnetic field due to long straight conductor carrying current
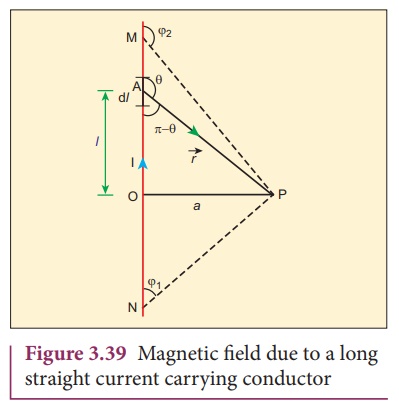
Consider a long straight wire NM with current I flowing from N to M as shown in Figure 3.39. Let P be the point at a distance a from point O. Consider an element of length dl of the wire at a distance l from point O and ![]() be the vector joining the element dl with the point P. Let ╬Ė be the angle between
be the vector joining the element dl with the point P. Let ╬Ė be the angle between ![]() and
and ![]() . Then, the magnetic field at P due to the element is
. Then, the magnetic field at P due to the element is
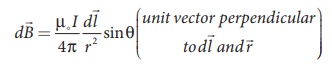
The direction of the field is perpendicular to the plane of the paper and going into it. This can be determined by taking the cross product between two vectors ![]() and
and ![]() (let it be n^ ). The net magnetic field can be determined by integrating equation (3.38) with proper limits.
(let it be n^ ). The net magnetic field can be determined by integrating equation (3.38) with proper limits.
From the Figure 3.39, in a right angle triangle PAO,
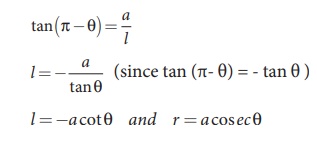
Differentiating,

This is the magnetic field at a point P due to the current in small elemental length. Note that we have expressed the magnetic field OP in terms of angular coordinate i.e. ╬Ė. Therefore, the net magnetic field at the point P which can be obtained by integrating d![]() by varying the angle from ╬Ė = Žå1 to ╬Ė = Žå2 is
by varying the angle from ╬Ė = Žå1 to ╬Ė = Žå2 is

For a an infinitely long straight wire, ŽĢ1 = 0 and ŽĢ2 = ŽĆ, the magnetic field is

Note that here n ^ represents the unit vector from the point O to P.
EXAMPLE 3.15
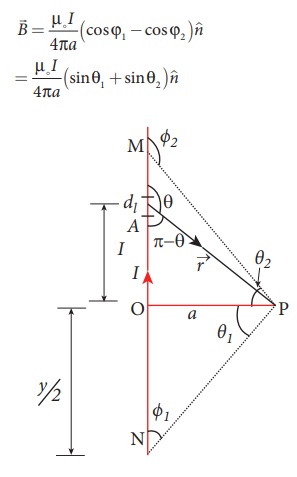
Calculate the magnetic field at a point P which is perpendicular bisector to current carrying straight wire as shown in figure.
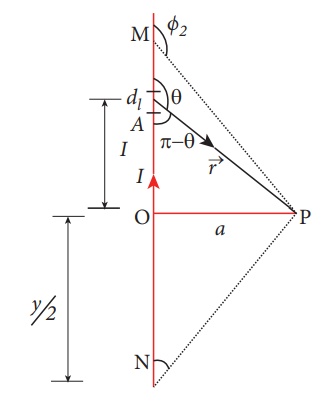
Solution
Let the length MN = y and the point P is on its perpendicular bisector. Let O be the point on the conductor as shown in figure.

The result obtained is same as we obtained in equation (3.39).
EXAMPLE 3.16
Show that for a straight conductor, the magnetic field
Solution:
In a right angle triangle OPN, let the angle ŌłĀ OPN = ╬Ė1 which implies, ŽĢ1 = ŽĆ /2 ŌłÆ ╬Ė1 and also in a right angle triangle OPM, ŌłĀOPM = ╬Ė2 which implies, ŽĢ2 = ŽĆ/2 + ╬Ė2
Hence,
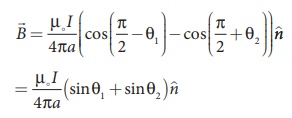
Related Topics