Toroid

Toroid

A solenoid is bent in such a way its ends are joined together to form a closed ring shape, is called a toroid which is shown in Figure 3.47. The magnetic field has constant magnitude inside the toroid whereas in the interior region (say, at point P) and exterior region (say, at point Q), the magnetic field is zero.

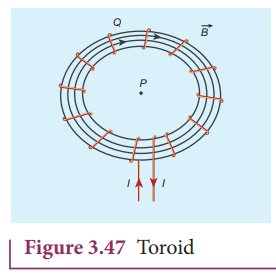
(a) Open space interior to the toroid

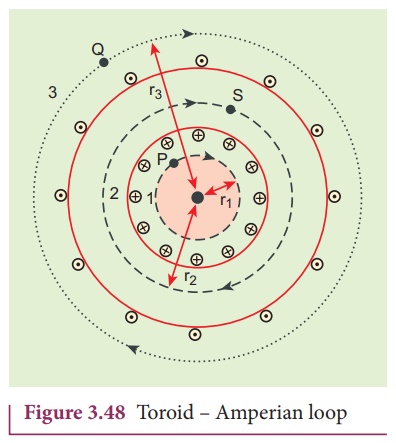
Let us calculate the magnetic field BP at point P. We construct an Amperian loop 1 of radius r1 around the point P as shown in Figure 3.48. For simplicity, we take circular loop so that the length of the loop is its circumference.

L1 = 2Ï€r1

Ampère’s circuital law for the loop 1 is

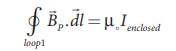
Since, the loop1 encloses no current, Ienclosed = 0

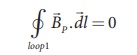
This is possible only if the magnetic field at point P vanishes i.e.

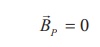
(b) Open space exterior to the toroid

Let us calculate the magnetic field BQ at point Q. We construct an Amperian loop 3 of radius r3 around the point Q as shown in Figure 3.48. The length of the loop is

L3 = 2Ï€r3

Ampère’s circuital law for the loop 3 is

Since, in each turn of the toroid loop, current coming out of the plane of paper is cancelled by the current going into the plane of paper. Thus, Ienclosed = 0

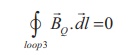
This is possible only if the magnetic field at point Q vanishes i.e.

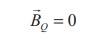
(c) Inside the toroid

Let us calculate the magnetic field BS at point S by constructing an Amperian loop 2 of radius r2 around the point S as shown in Figure 3.48. The length of the loop is

L2 = 2Ï€r2

Ampere’s circuital law for the loop 2 is

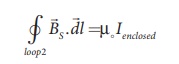
Let I be the current passing through the toroid and N be the number of turns of the toroid, then

The number of turns per unit length is n = N/2Ï€r2 , then the magnetic field at point S is