Force on a moving charge in a magnetic field

Force on a moving charge in a magnetic field

When an electric charge q is moving with velocity  in the magnetic field  , it experiences a force, called magnetic force  . After careful experiments, Lorentz deduced the force experienced by a moving charge in the magnetic field 

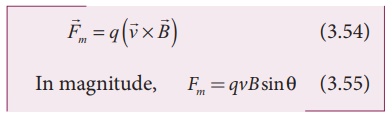
The equations (3.54) and (3.55) imply

1.   is directly proportional to the magnetic field 

2.   is directly proportional to the velocity 

3.   is directly proportional to sine of the angle between the velocity and magnetic field

4.   is directly proportional to the magnitude of the charge q

5. The direction of  is always perpendicular to  and as  is the cross product of  and 

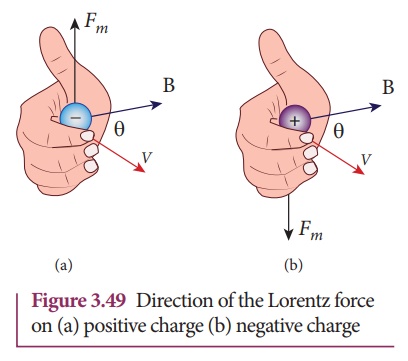
6. The direction of  on negative charge is opposite to the direction of  on positive charge provided other factors are identical as shown Figure 3.49

7. If velocity  of the charge q is along magnetic field  then,  is zero

Definition of tesla

The strength of the magnetic field is one tesla if unit charge moving in it with unit velocity experiences unit force.

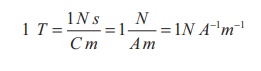
EXAMPLE 3.20

A particle of charge q moves with along positive y - direction invelocity  a magnetic field . Compute the Lorentz force experienced by the particle (a) when magnetic field is along positive y-direction (b) when magnetic field points in positive z - direction (c) when magnetic field is in zy - plane and making an angle θ with velocity of the particle. Mark the direction of magnetic force in each case.

Solution

Velocity of the particle is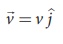 

(a) Magnetic field is along positive  y - direction, this implies,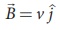 

From Lorentz force,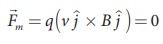 

So, no force acts on the particle when it moves along the direction of magnetic field.

(b) Magnetic field points in positive z - direction, this implies,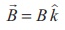 

From Lorentz force, 

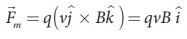
Therefore, the magnitude of the Lorentz force is qvB and direction is along positive x - direction.

(c) Magnetic field is in zy - plane and making an angle θ with the velocity of the particle, which implies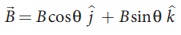 

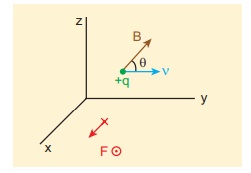
From Lorentz force,

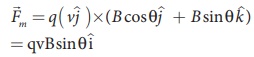
EXAMPLE 3.21

Compute the work done and power delivered by the Lorentz force on the particle of charge q moving with velocity  . Calculate the angle between Lorentz force and velocity of the charged particle and also interpret the result.

Solution

For a charged particle moving on a magnetic field,

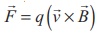
The work done by the magnetic field is

Since  is perpendicular to  and hence 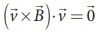 This means that Lorentz force do no work on the particle. From work kinetic energy theorem, (Refer section 4th chapter, XI th standard Volume I)

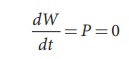
Since,  and  are perpendicular to each other. The angle between Lorentz force and velocity of the charged particle is 90º. Thus Lorentz force changes the direction of the velocity but not the magnitude of the velocity. Hence Lorentz force does no work and also does not alter kinetic energy of the particle.