Magnetic field due to a long current carrying solenoid

Magnetic field due to a long current carrying solenoid

Consider a solenoid of length L having N turns. The diametre of the solenoid is assumed to be much smaller when compared to its length and the coil is wound very closely.

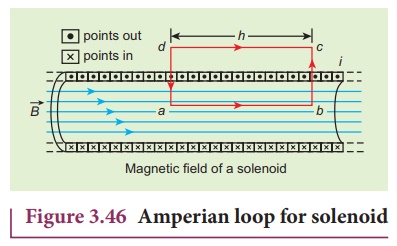
In order to calculate the magnetic field at any point inside the solenoid, we use Ampere’s circuital law. Consider a rectangular loop abcd as shown in Figure 3.46. Then from Ampère’s circuital law,

The left hand side of the equation is

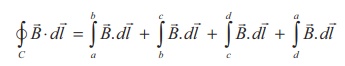
Since the elemental lengths along bc and da are perpendicular to the magnetic field which is along the axis of the solenoid, the integrals

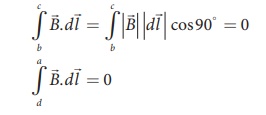
Since the magnetic field outside the solenoid is zero, the integral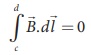 

For the path along ab, the integral is

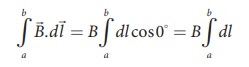
where the length of the loop ab as shown in the Figure 3.46 is h. But the choice of length of the loop ab is arbitrary. We can take very large loop such that it is equal to the length of the solenoid L. Therefore the integral is

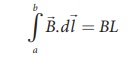
Let N I be the current passing through the solenoid of N turns, then

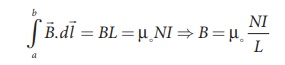
The number of turns per unit length is given by N/L = n, Then

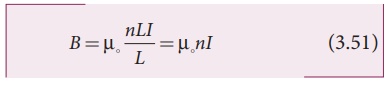
Since n is a constant for a given solenoid and μ0 is also constant. For a fixed current I, the magnetic field inside the solenoid is also a constant.

EXAMPLE 3.19

Calculate the magnetic field inside a solenoid, when

(a) the length of the solenoid becomes twice and fixed number of turns

(b) both the length of the solenoid and number of turns are double

(c) the number of turns becomes twice for the fixed length of the solenoid

Compare the results.

Solution

The magnetic field of a solenoid (inside) is

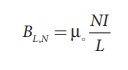
(a) length of the solenoid becomes twice and fixed number of turns

L→2L (length becomes twice)

N→N (number of turns are fixed)

The magnetic field is

B2L , N = µ NI/2L = 1/2 BL ,N

(b) both the length of the solenoid and number of turns are double

L→2L (length becomes twice)

N→2N (number of turns becomes twice)

The magnetic field is

(c) the number of turns becomes twice but for the fixed length of the solenoid

L→L (length is fixed)

N→2N (number of turns becomes twice)

The magnetic field is

BL ,2 N = µ, 2NI/L = 2BL ,N

From the above results,

BL ,2 N > B2 L ,2 N > B2 L , N

Thus, strength of the magnetic field is increased when we pack more loops into the same length for a given current.