Magnetic field produced along the axis of the current carrying circular coil

Magnetic field produced along the axis of the current carrying circular coil

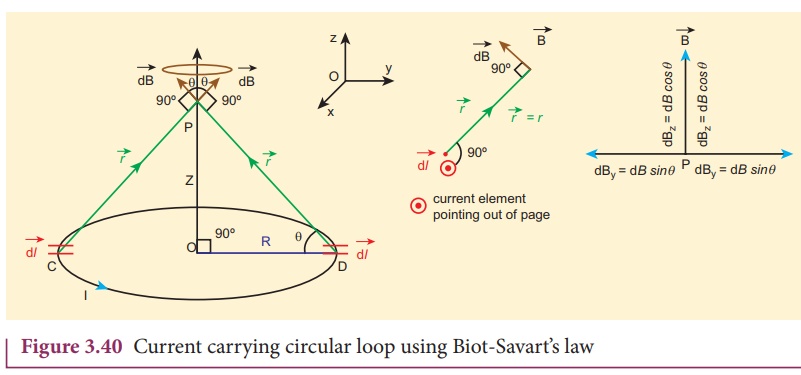
Consider a current carrying circular loop of radius R and let I be the current flowing through the wire in the direction as shown in Figure 3.40. The magnetic field at a point P on the axis of the circular coil at a distance z from its center of the coil O. It is computed by taking two diametrically opposite line elements of the coil each of length  at C and D. Let  be the vector joining the current element (I  ) at C to the point P.

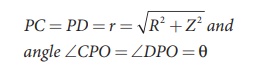
According to Biot-Savart’s law, the magnetic field at P due to the current element I is

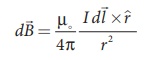
The magnitude of magnetic field due to current element I  at C and D are equal because of equal distance from the coil. The magnetic field d due to each current element I is resolved into two components; dB sin θ along y - direction and dB cos θ along z - direction. Horizontal components of each current element cancels out while the vertical components (dB cos θ  ) alone contribute to total magnetic field at the point P.

If we integrate  around the loop, d  sweeps out a cone as shown in Figure 3.40, then the net magnetic field  at point P is

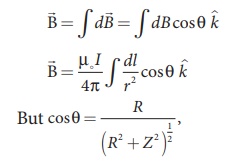
 using Pythagorous  theorem r2= R2+Z2 and integrating line element from 0 to 2Ï€R, we get

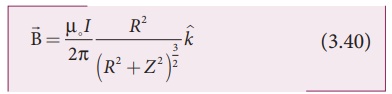
Note that the magnetic field  points along the direction from the point O to P. Suppose if the current flows in clockwise direction, then magnetic field points in the direction from the point P to O.

EXAMPLE 3.17

What is the magnetic field at the center of the loop shown in figure?

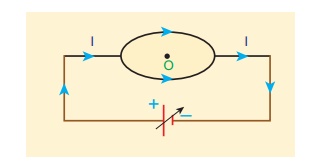
Solution

The magnetic field due to current in the upper hemisphere and lower hemisphere of the circular coil are equal in magnitude but opposite in direction. Hence, the net magnetic field at the center of the loop (at point O) is zero .