Lorentz Force | Physics - Motion of a charged particle in a uniform magnetic field | 12th Physics : Magnetism and Magnetic Effects of Electric Current
Chapter: 12th Physics : Magnetism and Magnetic Effects of Electric Current
Motion of a charged particle in a uniform magnetic field
Motion of a charged particle in a uniform magnetic field
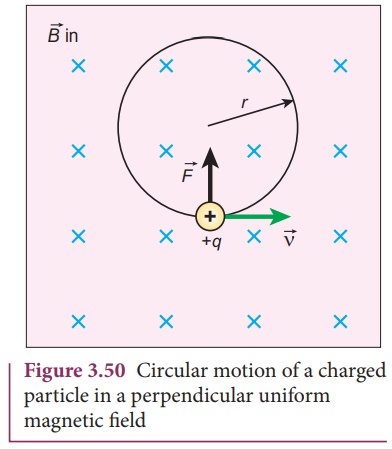
Consider a charged particle of charge q having mass m enters into a region of uniform magnetic field ![]() with velocity
with velocity ![]() such that velocity is perpendicular to the magnetic field. As soon as the particle enters into the field, Lorentz force acts on it in a direction perpendicular to both magnetic field
such that velocity is perpendicular to the magnetic field. As soon as the particle enters into the field, Lorentz force acts on it in a direction perpendicular to both magnetic field ![]() and velocity
and velocity ![]() .
.
As a result, the charged particle moves in a circular orbit as shown in Figure 3.50.
The Lorentz force on the charged particle is given by
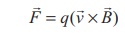
Since Lorentz force alone acts on the particle, the magnitude of the net force on the particle is
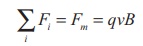
This Lorentz force acts as centripetal force for the particle to execute circular motion. Therefore,
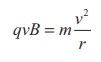
The radius of the circular path is

where p = mv is the magnitude of the linear momentum of the particle. Let T be the time taken by the particle to finish one complete circular motion, then

Hence substituting (3.56) in (3.57), we get

Equation (3.58) is called the cyclotron period. The reciprocal of time period is the frequency f, which is

In terms of angular frequency Žē,

Equations (3.59) and (3.60) are called as cyclotron frequency or gyro-frequency.
From equations (3.58), (3.59) and (3.60), we infer that time period and frequency depend only on charge-to-mass ratio (specific charge) but not velocity or the radius of the circular path.
If a charged particle moves in a region of uniform magnetic field such that its velocity is not perpendicular to the magnetic field, then the velocity of the particle is split up into two components; one component is parallel to the field while the other perpendicular to the field. The component of velocity parallel to field remains unchanged and the component perpendicular to field keeps changing due to the Lorentz force. Hence the path of the particle is not a circle; it is a helix around the field lines as shown in Figure 3.51.

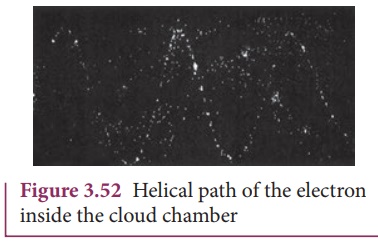
For an example, the helical path of an electron when it moves in a magnetic field is shown in Figure 3.52. Inside the particle detector called cloud chamber, the path is made visible by the condensation of water droplets.
EXAMPLE 3.22
An electron moving perpendicular to a uniform magnetic field 0.500 T undergoes circular motion of radius 2.80 mm. What is the speed of electron?
Solution
Charge of an electron q = -1.60 ├Ś 10-19 C
Ō¤╣ |q| = 1.60 ├Ś10ŌłÆ19 C
Magnitude of magnetic field B = 0.500 T
Mass of the electron, m = 9.11 ├Ś 10-31 kg
Radius of the orbit, r = 2.50 mm = 2.50 ├Ś 10-3 m
Velocity of the electron, v = |q| rB/m
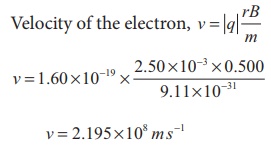
v = 2.195 ├Ś108 m sŌłÆ1
EXAMPLE 3.23
A proton moves in a uniform magnetic field of strength 0.500 T magnetic field is directed along the x-axis. At initial time, t = 0 s, the proton has velocity 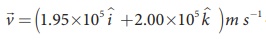 . Find
. Find
(a) At initial time, what is the acceleration of the proton.
(b) Is the path circular or helical?. If helical, calculate the radius of helical trajectory and also calculate the pitch of the helix (Note: Pitch of the helix is the distance travelled along the helix axis per revolution).
Solution

Pitch of the helix is the distance travelled along x-axis in a time T, which is P = vx T
But time,
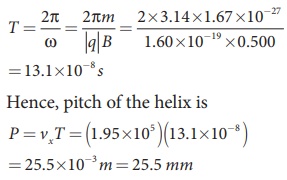
The proton experiences appreciable acceleration in the magnetic field, hence the pitch of the helix is almost six times greater than the radius of the helix.
EXAMPLE 3.24
Two singly ionized isotopes of uranium 23592U and 23892U (isotopes have same atomic number but different mass number) are sent with velocity 1.00 ├Ś 105 m s-1 into a magnetic field of strength 0.500 T normally. Compute the distance between the two isotopes after they complete a semi-circle. Also compute the time taken by each isotope to complete one semi-circular path. (Given: masses of the isotopes: m235 = 3.90 x 10-25 kg and m238 = 3.95 x 10-25 kg)
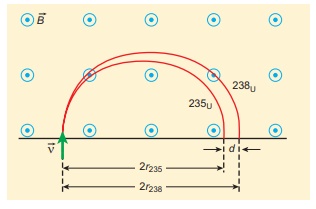
Solution
Since isotopes are singly ionized, they have equal charge which is equal to the charge of an electron, q = - 1.6 ├Ś 10-19 C. Mass of uranium 23592U and 23892U are 3.90 ├Ś 10-25 kg and 3.95 ├Ś 10-25 kg respectively. Magnetic field applied, B = 0.500 T. Velocity of the electron is 1.00 ├Ś 105 m s-1, then
(a) the radius of the path of 23592U is r235

The diameter of the semi-circle due to 23892U is d238 = 2r238 = 98.8 cm
Therefore the separation distance between the isotopes is ╬öd = d238 ŌłÆ d235 = 1.2cm
(b) The time taken by each isotope to complete one semi-circular path are

Note that even though the difference between mass of two isotopes are very small, this arrangement helps us to convert this small difference into an easily measurable distance of separation. This arrangement is known as mass spectrometer. A mass spectrometer is used in many areas in sciences, especially in medicine, in space science, in geology etc. For example, in medicine, anaesthesiologists use it to measure the respiratory gases and biologist use it to determine the reaction mechanisms in photosynthesis.
Related Topics