Motion of a charged particle under crossed electric and magnetic field (velocity selector)

Motion of a charged particle under crossed electric and magnetic field (velocity selector)

Consider an electric charge q of mass m which enters into a region of uniform magnetic field  with velocity  such that velocity is not perpendicular to the magnetic field. Then the path of the particle is a helix. The Lorentz force on the charged particle moving in a uniform magnetic field can be balanced by Coulomb force by proper arrangement of electric and magnetic fields.

The Coulomb force acts along the direction of electric field (for a positive charge q) whereas the Lorentz force is perpendicular to the direction of magnetic field. Therefore in order to balance these forces, both electric and magnetic fields must be perpendicular to each other. Such an arrangement of perpendicular electric and magnetic fields are known as cross fields.

 For illustration, consider an experimental arrangement as shown in Figure 3.53. In the region of space between parallel plates of a capacitor (which produces uniform electric field), uniform magnetic field is maintained perpendicular to the direction of electric field. Suppose a charged particle enters this space from the left side as shown, the net force on the particle is

For a positive charge, the electric force on the charge acts in downward direction whereas the Lorentz force acts upwards. When these two forces balance one another, then

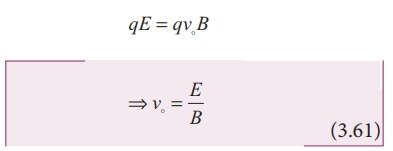
This means, for a given magnitude of - field and - field, the forces act only for the particle moving with particular speed v0 = E/B . This speed is independent of mass and charge.

If the charge enters into the crossed fields with velocity v, other than vo, it results in any of the following possibilities (Table 3.4).

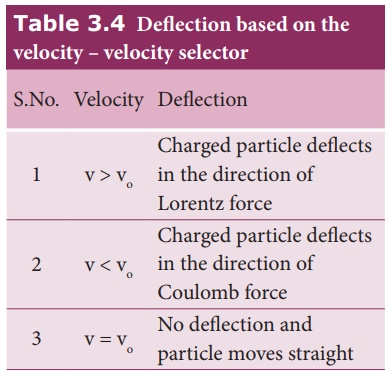
So by proper choice of electric and magnetic fields, the particle with particular speed can be selected. Such an arrangement of fields is called a velocity selector.

EXAMPLE 3.25

Let E be the electric field of magnitude 6.0 × 106 N C-1 and B be the magnetic field magnitude 0.83 T. Suppose an electron is accelerated with a potential of 200 V, will it show zero deflection?. If not, at what potential will it show zero deflection.

Solution:

Electric field, E = 6.0 × 106 N C-1 and magnetic field, B = 0.83 T.

Then

When an electron goes with this velocity, it shows null deflection. Since the accelerating potential is 200 V, the electron acquires kinetic energy because of this accelerating potential. Hence,

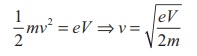
Since the mass of the electron, m = 9 .1×10−31 kg and charge of an electron, |q| = e = 1.6 ×10−19 C. The velocity due to accelerating potential 200 V

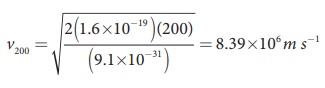
Since the speed v200 > v, the electron is deflected towards direction of Lorentz force. So, in order to have null deflection, the potential, we have to supply is

V =148 65 V