Biot - Savart Law

BIOT - SAVART LAW

Soon after the Oersted’s discovery, both Jean-Baptiste Biot and Felix Savart in 1819 did quantitative experiments on the force experienced by a magnet kept near current carrying wire and arrived at a mathematical expression that gives the magnetic field at some point in space in terms of the current that produces the magnetic field. This is true for any shape of the conductor.

1. Definition and explanation of Biot- Savart law

Biot and Savart experimentally observed that the magnitude of magnetic field d at a point P (Figure 3.37) at a distance r from the small elemental length taken on a conductor carrying current varies

 i.directly as the strength of the current I

  ii.directly as the magnitude of the length element 

  iii.directly as the sine of the angle (say,θ) between  and r ^ .

  iv.inversely as the square of the distance between the point P and length element .

This is expressed as

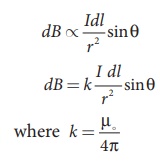
in SI units and k = 1 in CGS units. In vector notation, 

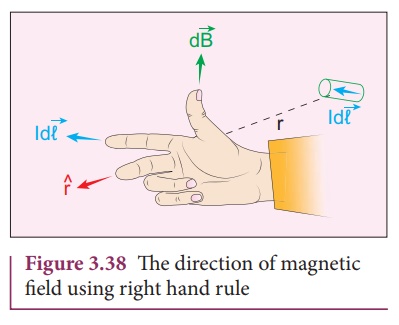
Here vector d is perpendicular to both I  (pointing the direction of current flow) and the unit vector r ^ directed from  toward point P (Figure 3.38).

The equation (3.37) is used to compute the magnetic field only due to a small elemental length dl of the conductor. The net magnetic field at P due to the conductor is obtained from principle of superposition by considering the contribution from all current elements I  . Hence integrating equation (3.37), we get

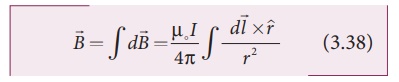
where the integral is taken over the entire current distribution.

Cases

1.     If the point P lies on the conductor, then θ = 0º. Therefore, d  is zero.

2.     If the point lies perpendicular to the conductor, then θ = 90º. Therefore, d  is maximum and is given by 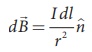 where  is the unit vector perpendicular to both I  and .

Similarities between Coulomb’s law and Biot-Savort’s law

Electric and magnetic fields

·        obey inverse square law, so they are long range fields.

·        obey the principle of superposition and are linear with respect to source. In magnitude,

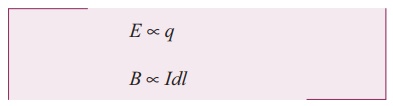
Note that the exponent of charge q (source) and exponent of electric field E is unity. Similarly, the exponent of current element Idl (source) and exponent of magnetic field B is unity. In other words, electric field  is proportional only to charge (source) and not on higher powers of charge ( q² , q³ , etc). Similarly, magnetic field  is proportional to current element I (source) and not on square or cube or higher powers of current element. The cause and effect have linear relationship.

2. Magnetic field due to long straight conductor carrying current

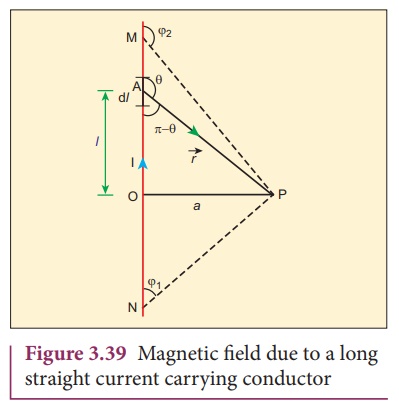
Consider a long straight wire NM with current I flowing from N to M as shown in Figure 3.39. Let P be the point at a distance a from point O. Consider an element of length dl of the wire at a distance l from point O and  be the vector joining the element dl with the point P. Let θ be the angle between  and  . Then, the magnetic field at P due to the element is

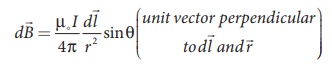
The direction of the field is perpendicular to the plane of the paper and going into it. This can be determined by taking the cross product between two vectors  and  (let it be n^ ). The net magnetic field can be determined by integrating equation (3.38) with proper limits.

From the Figure 3.39, in a right angle triangle PAO,

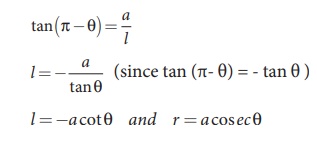
Differentiating,

This is the magnetic field at a point P due to the current in small elemental length. Note that we have expressed the magnetic field OP in terms of angular coordinate i.e. θ. Therefore, the net magnetic field at the point P which can be obtained by integrating d by varying the angle from θ = φ₁ to θ = φ₂ is

For a an infinitely long straight wire, Ï•₁ = 0 and Ï•₂ = Ï€, the magnetic field is

Note that here n ^ represents the unit vector from the point O to P.

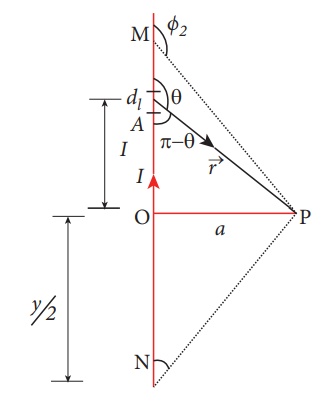
EXAMPLE 3.15

Calculate the magnetic field at a point P which is perpendicular bisector to current carrying straight wire as shown in figure.

Solution

Let the length MN = y and the point P is on its perpendicular bisector. Let O be the point on the conductor as shown in figure.

The result obtained is same as we obtained in equation (3.39).

EXAMPLE 3.16

Show that for a straight conductor, the magnetic field

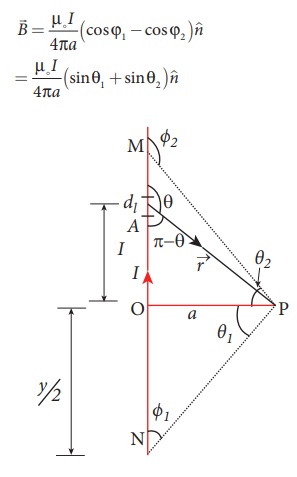
Solution:

In a right angle triangle OPN, let the angle ∠ OPN = θ₁ which implies, Ï•₁ = Ï€ /2  − θ₁ and also in a right angle triangle OPM, ∠OPM = θ₂ which implies, Ï•₂ = Ï€/2 + θ₂

Hence,

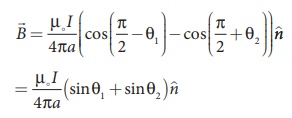
3. Magnetic field produced along the axis of the current carrying circular coil

Consider a current carrying circular loop of radius R and let I be the current flowing through the wire in the direction as shown in Figure 3.40. The magnetic field at a point P on the axis of the circular coil at a distance z from its center of the coil O. It is computed by taking two diametrically opposite line elements of the coil each of length  at C and D. Let  be the vector joining the current element (I  ) at C to the point P.

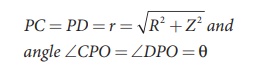
According to Biot-Savart’s law, the magnetic field at P due to the current element I is

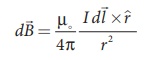
The magnitude of magnetic field due to current element I  at C and D are equal because of equal distance from the coil. The magnetic field d due to each current element I is resolved into two components; dB sin θ along y - direction and dB cos θ along z - direction. Horizontal components of each current element cancels out while the vertical components (dB cos θ  ) alone contribute to total magnetic field at the point P.

If we integrate  around the loop, d  sweeps out a cone as shown in Figure 3.40, then the net magnetic field  at point P is

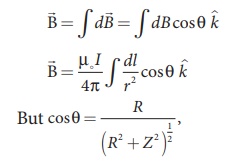
 using Pythagorous  theorem r²= R²+Z² and integrating line element from 0 to 2Ï€R, we get

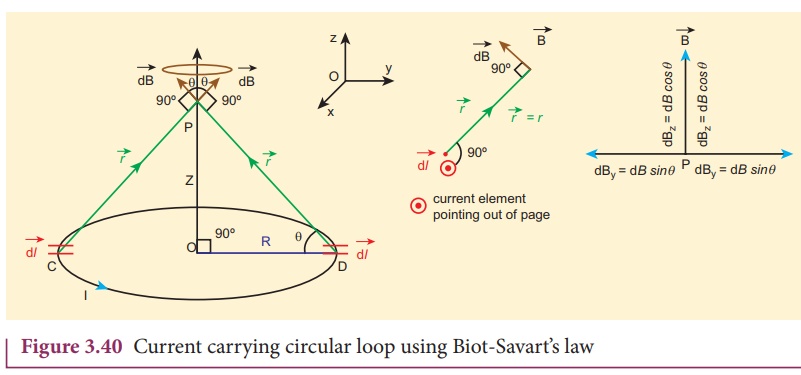
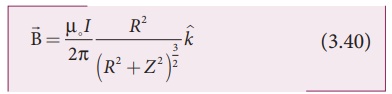
Note that the magnetic field  points along the direction from the point O to P. Suppose if the current flows in clockwise direction, then magnetic field points in the direction from the point P to O.

EXAMPLE 3.17

What is the magnetic field at the center of the loop shown in figure?

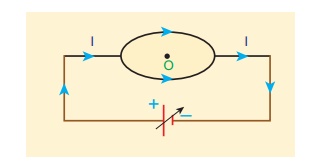
Solution

The magnetic field due to current in the upper hemisphere and lower hemisphere of the circular coil are equal in magnitude but opposite in direction. Hence, the net magnetic field at the center of the loop (at point O) is zero .

4. Current loop as a magnetic dipole

The magnetic field from the centre of a circular loop of radius R along the axis is given by

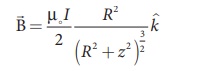
At larger distance Z >> R, therefore R² + Z²  ≈ Z² , we have

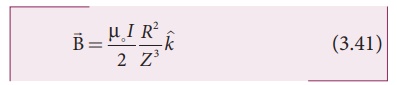
Let A be the area of the circular loop A = Ï€ R². So rewriting the equation (3.41) in terms of area of the loop, we have

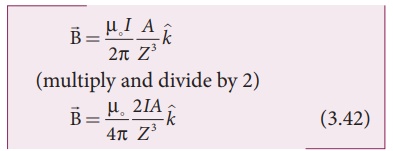
Comparing equation (3.42)   with equation (3.14) dimensionally, we get

p_m = I A

where p_m is called magnetic dipole moment. In vector notation,

This implies that a current carrying circular loop behaves as a magnetic dipole of magnetic moment _m . So, the magnetic dipole moment of any current loop is equal to the product of the current and area of the loop.

Right hand thumb rule

In order to determine the direction of magnetic moment, we use right hand thumb rule (mnemonic) which states that

If we curl the fingers of right hand in the direction of current in the loop, then the stretched thumb gives the direction of the magnetic moment associated with the loop.

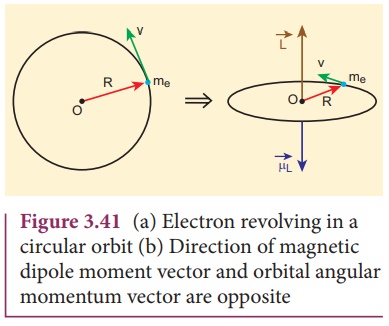
5. Magnetic dipole moment of revolving electron

Suppose an electron undergoes circular motion around the nucleus as shown in Figure 3.41. The circulating electron in a loop is like current in a circular loop (since flow of charge is current). The magnetic dipole moment due to current carrying circular loop is

In magnitude,

µ_L = I A

If T is the time period of an electron, the current due to circular motion of the electron is

where −e is the charge of an electron. If R is the radius of the circular orbit and v is the velocity of the the velocity of the electron in the circular orbit, then

Using equation (3.45) and equation (3.46) in equation (3.44), we get

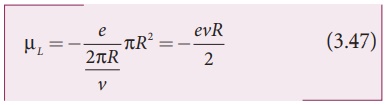
where A = Ï€R² is the area of the circular loop. By definition, angular momentum of the electron about O is

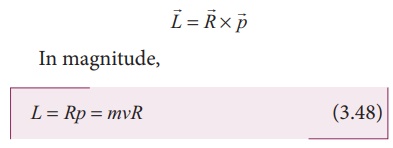
Using equation (3.47)  and  equation (3.48), we get               

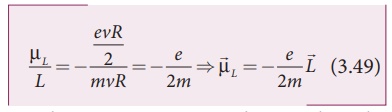
The negative sign indicates that the magnetic moment and angular momentum are in opposite direction.

In magnitude,

The ratio µ_L/L is a constant and also known as gyro-magnetic ratio (e/2m). It must be noted that the gyro-magnetic ratio is a constant of proportionality which connects angular momentum of the electron and the magnetic moment of the electron.

According to Neil’s Bohr quantization rule, the angular momentum of an electron moving in a stationary orbit is quantized, which means,

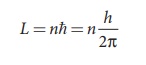
where, h is the Planck’s constant (h = 6.63 x 10^-34 J s ) and number n takes natural numbers

(i.e., n = 1,2,3,....). Hence,

The minimum magnetic moment can be obtained by substituting n = 1,

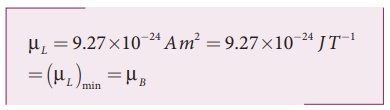
where, µ_B =eh/4Ï€m= 9.27 ×10^−24 Am²  is called Bohr magneton. This is a convenient unit with which one can measure atomic magnetic moments.

Note: Bohr quantization rule will be discussed in unit 8 of second volume