Introduction to Magnetism

INTRODUCTION TO MAGNETISM

Magnets! no doubt, its behaviour will attract everyone (see Figure 3.1). The world enjoys its benefits, to lead a modern luxurious life. The study of magnets fascinated scientists around our globe for many centuries and even now, door for research on magnets is still open.

Magnetism is everywhere from tiny particles like electrons to the entire universe. Historically the word ‘magnetism’ was derived from iron ore magnetite (Fe₃ O₄). In olden days, magnets were used as magnetic compass for navigation, magnetic therapy for treatment and also used in magic shows.

In modern days, most of the things we use in our daily life contain magnets (Figure 3.2). Motors, cycle dynamo, loudspeakers, magnetic tapes used in audio and video recording, mobile phones, head phones, CD, pen-drive, hard disc of laptop, refrigerator door, generator are a few examples.

Earlier, both electricity and magnetism were thought to be two independent branches in physics. In 1820, H.C. Oersted observed the deflection of magnetic compass needle kept near a current carrying wire. This unified the two different branches, electricity and magnetism as a single subject ‘electromagnetism’ in physics.

In this unit, basics of magnets and their properties are given. Later, how a current carrying conductor (here only steady current, not time-varying current is considered) behaves like a magnet is presented.

1. Earth’s magnetic field and magnetic elements

From the activities performed in lower classes, we have noticed that the needle in a magnetic compass or freely suspended magnet comes to rest in a position which is approximately along the geographical north-south direction of the Earth. William Gilbert in 1600 proposed that Earth itself behaves like a gigantic powerful bar magnet.

But this theory is not successful because the temperature inside the Earth is very high and so it will not be possible for a magnet to retain its magnetism.

Gover suggested that the Earth’s magnetic field is due to hot rays coming out from the Sun. These rays will heat up the air near equatorial region. Once air becomes hotter, it rises above and will move towards northern and southern hemispheres and get electrified. This may be responsible to magnetize the ferromagnetic materials near the Earth’s surface. Till date, so many theories have been proposed. But none of the theory completely explains the cause for the Earth’s magnetism.

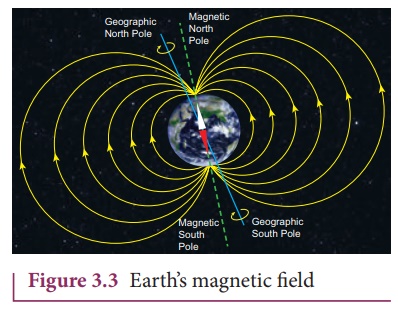
The north pole of magnetic compass needle is attracted towards the magnetic south pole of the Earth which is near the geographic north pole (Figure 3.3). Similarly, the south pole of magnetic compass needle is attracted towards the geographic north pole of the Earth which is near magnetic north-pole. The branch of physics which deals with the Earth’s magnetic field is called Geomagnetism or Terrestrial magnetism.

There are three quantities required to specify the magnetic field of the Earth on its surface, which are often called as the elements of the Earth’s magnetic field. They are

(a) magnetic declination (D)

(b) magnetic dip or inclination (I)

(c) the horizontal component of the Earth’s magnetic field (B_H)

Day and night occur because Earth spins about an axis called geographic axis. A vertical plane passing through the geographic axis is called geographic meridian and a great circle perpendicular to Earth’s geographic axis is called geographic equator.

The straight line which connects magnetic poles of Earth is known as magnetic axis. A vertical plane passing through magnetic axis is called magnetic meridian and a great circle perpendicular to Earth’s magnetic axis is called magnetic equator.

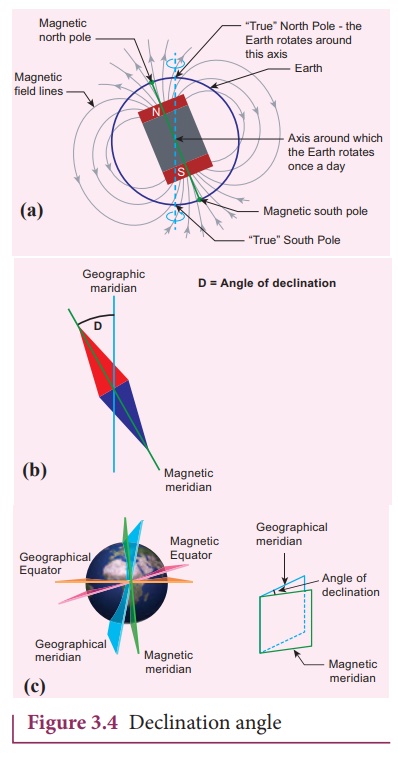
When a magnetic needle is freely suspended, the alignment of the magnet does not exactly lie along the geographic meridian as shown in Figure 3.4. The angle between magnetic meridian at a point and geographical meridian is called the declination or magnetic declination (D). At higher latitudes, the declination is greater whereas near the equator, the declination is smaller. In India, declination angle is very small and for Chennai, magnetic declination angle is -1º 8’ (which is negative (west)).

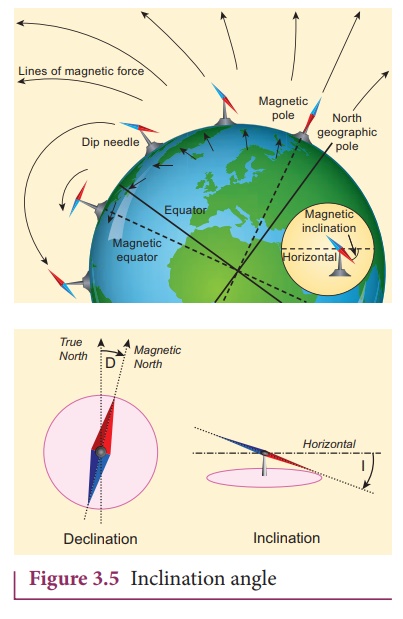
The angle subtended by the Earth’s total magnetic field  with the horizontal direction in the magnetic meridian is called dip or magnetic inclination (I) at that point (Figure 3.5). For Chennai, inclination angle is 14o 16’. The component of Earth’s magnetic field along the horizontal direction in the magnetic meridian is called horizontal component of Earth’s magnetic field, denoted by B_H.

Let B_E be the net Earth’s magnetic field at a point P on the surface of the Earth. B_E can be resolved into two perpendicular components.

(i) At magnetic equator

The Earth’s magnetic field is parallel to the surface of the Earth (i.e., horizontal) which implies that the needle of magnetic compass rests horizontally at an angle of dip, I = 0o as shown in figure 3.6.

B_H = B_E

B_V = 0

This implies that the horizontal component is maximum at equator and vertical component is zero at equator.

(ii) At magnetic poles

The Earth’s magnetic field is perpendicular to the surface of the Earth (i.e., vertical) which implies that the needle of magnetic compass rests vertically at an angle of dip, I = 90º as shown in Figure 3.7. Hence,

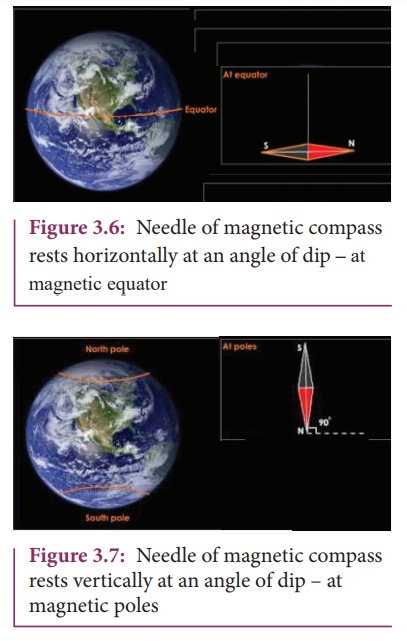
B_H = 0

B_V = B_E

This implies that the vertical component is maximum at poles and horizontal component is zero at poles.

EXAMPLE 3.1

The horizontal component and vertical components of Earth’s magnetic field at a place are 0.15 G and 0.26 G respectively. Calculate the angle of dip and resultant magnetic field.

Solution:

B_H = 0.15 G and B_V = 0.26 G

tan I = 00.26/0.15 ⇒ I = tan ^−1(1. 732) =60º 

The resultant magnetic field of the Earth is

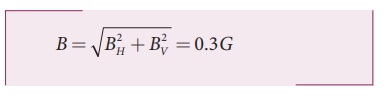
2. Basic properties of magnets

Some basic terminologies and properties used in describing bar magnet.

(a) Magnetic dipole moment

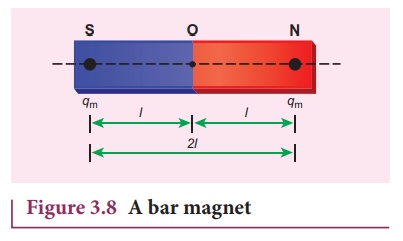
Consider a bar magnet as shown in Figure 3.8. Let q_m be the pole strength (it is also called as magnetic charge) of the magnetic pole and let l be the distance between the geometrical center of bar magnet O and one end of the pole. The magnetic dipole moment is defined as the product of its pole strength and magnetic length. It is a vector quantity, denoted by _m.

where  is the vector drawn from south pole to north pole and its magnitude ||2l .

The magnitude of magnetic dipole moment is p_m = 2q_m l

The SI unit of magnetic moment is A m2. Note that the direction of magnetic moment is from South pole to North pole.

(b) Magnetic field

Magnetic field is the region or space around every magnet within which its influence can be felt by keeping another magnet in that region. The magnetic field  at a point is defined as a force experienced by the bar magnet of unit pole strength.

Its unit is N A^-1 m^-1.

(c) Types of magnets 

Magnets are classified into natural magnets and artificial magnets. For example, iron, cobalt, nickel, etc. are natural magnets. Strengths of natural magnets are very weak and the shapes of the magnet are irregular. Artificial magnets are made by us in order to have desired shape and strength. If the magnet is in the form of rectangular shape or cylindrical shape, then it is known as bar magnet.

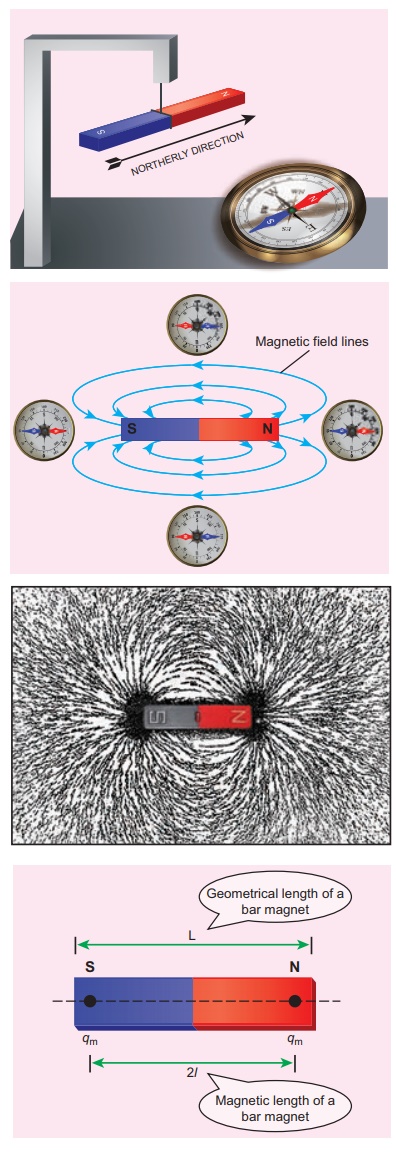
Properties of magnet

The following are the properties of bar magnet (Figure 3.9)

1. A freely suspended bar magnet will always point along the north-south direction.

2. A magnet attracts another magnet or magnetic substances towards itself. The attractive force is maximum near the end of the bar magnet. When a bar magnet is dipped into iron filling, they cling to the ends of the magnet.

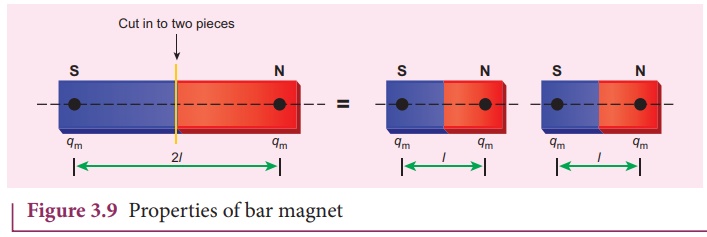
3. When a magnet is broken into pieces, each piece behaves like a magnet with poles at its ends.

4. Two poles of a magnet have pole strength equal to one another.

5. The length of the bar magnet is called geometrical length and the length between two magnetic poles in a bar magnet is called magnetic length. Magnetic length is always slightly smaller than geometrical length. The ratio of magnetic length and geometrical length is 5/6 .

Magnetic length / Geometricallength = 5/6 = 0.833

EXAMPLE 3.2

Let the magnetic moment of a bar magnet be m whose magnetic length is d = 2l and pole strength is q_m. Compute the magnetic moment of the bar magnet when it is cut into two pieces

(a) along its length

(b) perpendicular to its length.

Solution

(a) a bar magnet cut into two pieces along its length:

When the bar magnet is cut along the axis into two pieces, new magnetic pole strength is q′m = q_m/2 but magnetic length does not change. So, the magnetic moment is

In vector notation,

(b) a bar magnet cut into two pieces perpendicular to the axis:

When the bar magnet is cut perpendicular to the axis into two pieces, magnetic pole strength will not change but magnetic length will be halved. So the magnetic moment is

EXAMPLE 3.3

Compute the magnetic length of a uniform bar magnet if the geometrical length of the magnet is 12 cm. Mark the positions of magnetic pole points.

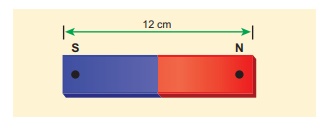
Solution

Geometrical length of the bar magnet is 12 cm

Magnetic length = 5/6 x (geometrical length)

= 5/6 x 12 = 10cm

In this figure, the dot implies the pole points.

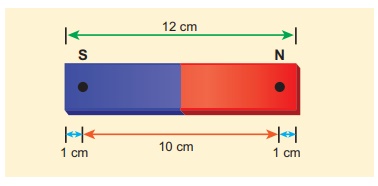
Magnetic field lines

1. Magnetic field lines are continuous closed curves. The direction of magnetic field lines is from North pole to South pole outside the magnet (Figure 3.10) and South pole to North pole inside the magnet.

2. The direction of magnetic field at any point on the curve is known by drawing tangent to the magnetic line of force at that point. In the Figure No. 3.10 (b), the tangent drawn at points P, Q and R gives the direction of magnetic field B at that point.

3. Magnetic field lines never intersect each other. Otherwise, the magnetic compass needle would point towards two directions, which is not possible.

4. The degree of closeness of the field lines determines the relative strength of the magnetic field. The magnetic field is strong where magnetic field lines crowd and weak where magnetic field lines thin out.

(d) Magnetic flux

The number of magnetic field lines crossing per unit area is called magnetic flux Φ_B. Mathematically, the magnetic flux through a surface of area A in a uniform magnetic field is defined as

where θ is the angle between B and A as shown in Figure 3.11.

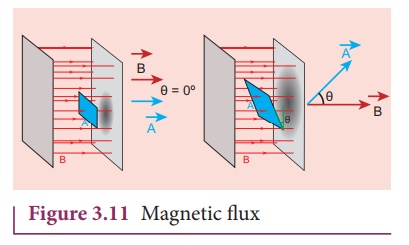
Special cases

When  is normal to the surface i.e., θ = 0º, the magnetic flux is Φ_B = BA (maximum).

When  is parallel to the surface i.e., θ = 90º, the magnetic flux is Φ_B = 0.

Suppose the magnetic field is not uniform over the surface, the equation (3.6) can be written as

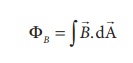
Magnetic flux is a scalar quantity. The SI unit for magnetic flux is weber, which is denoted by symbol Wb. Dimensional formula for magnetic flux is ML²T ^-2 A^-1 . The CGS unit of magnetic flux is Maxwell.

1 weber = 10⁸ maxwell

The magnetic flux density can also be defined as the number of magnetic field lines crossing unit area kept normal to the direction of line of force. Its unit is Wb m^-2 or tesla.

(e) Uniform magnetic field and Non-uniform magnetic field

Uniform magnetic field

Magnetic field is said to be uniform if it has same magnitude and direction at all the points in a given region. Example, locally Earth’s magnetic field is uniform.

The magnetic field of Earth has same value over the entire area of your school!

Non-uniform magnetic field

Magnetic field is said to be non-uniform if the magnitude or direction or both varies at all its points. Example: magnetic field of a bar magnet

EXAMPLE 3.4

Calculate the magnetic flux coming out from the surface containing magnetic dipole (say, a bar magnet) as shown in figure.

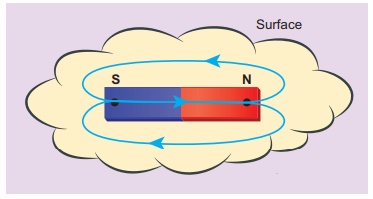
Solution

Magnetic dipole is kept, the total flux emanating from the closed surface S is zero. So,

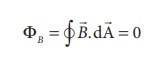
Here the integral is taken over closed surface. Since no isolated magnetic pole (called magnetic monopole) exists, this integral is always zero,

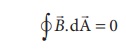
This is similar to Gauss’s law in electrostatics. (Refer unit 1)