Physics - Lorentz Force: Solved Example Problems | 12th Physics : Magnetism and Magnetic Effects of Electric Current
Chapter: 12th Physics : Magnetism and Magnetic Effects of Electric Current
Lorentz Force: Solved Example Problems
1. Force on a moving charge in a magnetic field: Solved Example Problems
EXAMPLE 3.20
A particle of charge q moves with along positive y - direction invelocity ![]() a magnetic field
a magnetic field ![]() . Compute the Lorentz force experienced by the particle (a) when magnetic field is along positive y-direction (b) when magnetic field points in positive z - direction (c) when magnetic field is in zy - plane and making an angle ╬Ė with velocity of the particle. Mark the direction of magnetic force in each case.
. Compute the Lorentz force experienced by the particle (a) when magnetic field is along positive y-direction (b) when magnetic field points in positive z - direction (c) when magnetic field is in zy - plane and making an angle ╬Ė with velocity of the particle. Mark the direction of magnetic force in each case.
Solution
Velocity of the particle is 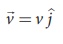
(a) Magnetic field is along positive y - direction, this implies, 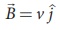

From Lorentz force, 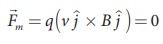
So, no force acts on the particle when it moves along the direction of magnetic field.
(b) Magnetic field points in positive z - direction, this implies, 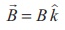

From Lorentz force,
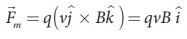
Therefore, the magnitude of the Lorentz force is qvB and direction is along positive x - direction.
(c) Magnetic field is in zy - plane and making an angle ╬Ė with the velocity of the particle, which implies 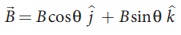
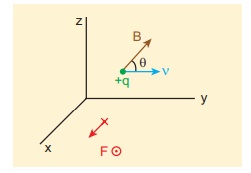
From Lorentz force,
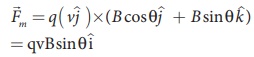
EXAMPLE 3.21
Compute the work done and power delivered by the Lorentz force on the particle of charge q moving with velocity ![]() . Calculate the angle between Lorentz force and velocity of the charged particle and also interpret the result.
. Calculate the angle between Lorentz force and velocity of the charged particle and also interpret the result.
Solution
For a charged particle moving on a magnetic field,
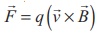
The work done by the magnetic field is

Since ![]() is perpendicular to
is perpendicular to ![]() and hence
and hence 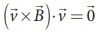 This means that Lorentz force do no work on the particle. From work kinetic energy theorem, (Refer section 4th chapter, XI th standard Volume I)
This means that Lorentz force do no work on the particle. From work kinetic energy theorem, (Refer section 4th chapter, XI th standard Volume I)
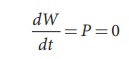
Since,  and
and ![]() are perpendicular to each other. The angle between Lorentz force and velocity of the charged particle is 90┬║. Thus Lorentz force changes the direction of the velocity but not the magnitude of the velocity. Hence Lorentz force does no work and also does not alter kinetic energy of the particle.
are perpendicular to each other. The angle between Lorentz force and velocity of the charged particle is 90┬║. Thus Lorentz force changes the direction of the velocity but not the magnitude of the velocity. Hence Lorentz force does no work and also does not alter kinetic energy of the particle.
2. Motion of a charged particle in a uniform magnetic field: Solved Example Problems
EXAMPLE 3.22
An electron moving perpendicular to a uniform magnetic field 0.500 T undergoes circular motion of radius 2.80 mm. What is the speed of electron?
Solution
Charge of an electron q = -1.60 ├Ś 10-19 C
Ō¤╣ |q| = 1.60 ├Ś10ŌłÆ19 C
Magnitude of magnetic field B = 0.500 T
Mass of the electron, m = 9.11 ├Ś 10-31 kg
Radius of the orbit, r = 2.50 mm = 2.50 ├Ś 10-3 m
Velocity of the electron, v = |q| rB/m
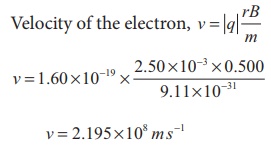
v = 2.195 ├Ś108 m sŌłÆ1
EXAMPLE 3.23
A proton moves in a uniform magnetic field of strength 0.500 T magnetic field is directed along the x-axis. At initial time, t = 0 s, the proton has velocity 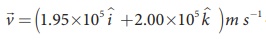 . Find
. Find
(a) At initial time, what is the acceleration of the proton.
(b) Is the path circular or helical?. If helical, calculate the radius of helical trajectory and also calculate the pitch of the helix (Note: Pitch of the helix is the distance travelled along the helix axis per revolution).
Solution

Pitch of the helix is the distance travelled along x-axis in a time T, which is P = vx T
But time,
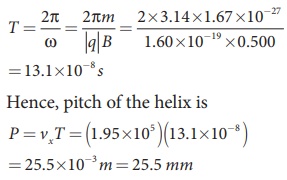
The proton experiences appreciable acceleration in the magnetic field, hence the pitch of the helix is almost six times greater than the radius of the helix.
EXAMPLE 3.24
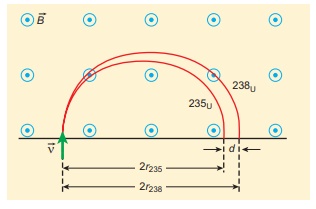
Two singly ionized isotopes of uranium 23592U and 23892U (isotopes have same atomic number but different mass number) are sent with velocity 1.00 ├Ś 105 m s-1 into a magnetic field of strength 0.500 T normally. Compute the distance between the two isotopes after they complete a semi-circle. Also compute the time taken by each isotope to complete one semi-circular path. (Given: masses of the isotopes: m235 = 3.90 x 10-25 kg and m238 = 3.95 x 10-25 kg)
Solution
Since isotopes are singly ionized, they have equal charge which is equal to the charge of an electron, q = - 1.6 ├Ś 10-19 C. Mass of uranium 23592U and 23892U are 3.90 ├Ś 10-25 kg and 3.95 ├Ś 10-25 kg respectively. Magnetic field applied, B = 0.500 T. Velocity of the electron is 1.00 ├Ś 105 m s-1, then
(a) the radius of the path of 23592U is r235

The diameter of the semi-circle due to 23892U is d238 = 2r238 = 98.8 cm
Therefore the separation distance between the isotopes is ╬öd = d238 ŌłÆ d235 = 1.2cm
(b) The time taken by each isotope to complete one semi-circular path are

Note that even though the difference between mass of two isotopes are very small, this arrangement helps us to convert this small difference into an easily measurable distance of separation. This arrangement is known as mass spectrometer. A mass spectrometer is used in many areas in sciences, especially in medicine, in space science, in geology etc. For example, in medicine, anaesthesiologists use it to measure the respiratory gases and biologist use it to determine the reaction mechanisms in photosynthesis.
3. Motion of a charged particle under crossed electric and magnetic field (velocity selector): Solved Example Problems
EXAMPLE 3.25
Let E be the electric field of magnitude 6.0 ├Ś 106 N C-1 and B be the magnetic field magnitude 0.83 T. Suppose an electron is accelerated with a potential of 200 V, will it show zero deflection?. If not, at what potential will it show zero deflection.
Solution:
Electric field, E = 6.0 ├Ś 106 N C-1 and magnetic field, B = 0.83 T.
Then

When an electron goes with this velocity, it shows null deflection. Since the accelerating potential is 200 V, the electron acquires kinetic energy because of this accelerating potential. Hence,
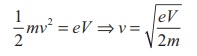
Since the mass of the electron, m = 9 .1├Ś10ŌłÆ31 kg and charge of an electron, |q| = e = 1.6 ├Ś10ŌłÆ19 C. The velocity due to accelerating potential 200 V
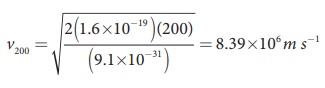
Since the speed v200 > v, the electron is deflected towards direction of Lorentz force. So, in order to have null deflection, the potential, we have to supply is

V =148 65 V
4. Cyclotron: Solved Example Problems
EXAMPLE 3.26
Suppose a cyclotron is operated to accelerate protons with a magnetic field of strength 1 T. Calculate the frequency in which the electric field between two Dees could be reversed.
Solution
Magnetic field B = 1 T
Mass of the proton, mp = 1.67 ├Ś10ŌłÆ27 kg
Charge of the proton, q = 1.60 ├Ś10ŌłÆ19 C
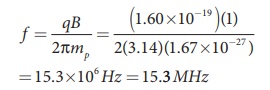
5. Force on a current carrying conductor placed in a magnetic field: Solved Example Problems
EXAMPLE 3.27
A metallic rod of linear density is 0.25 kg m-1 is lying horizontally on a smooth inclined plane which makes an angle of 45┬║ with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of strength 0.25 T is acting on it in the vertical direction. Calculate the electric current flowing in the rod to keep it stationary.
Solution
The linear density of the rod i.e., mass per unit length of the rod is 0.25 kg m-1
ŌćÆ m/l = 0.25 kg mŌłÆ1
Let I be the current flowing in the metallic rod. The direction of electric current is into the paper. The direction of magnetic force IBl is given by FlemingŌĆÖs left hand rule.
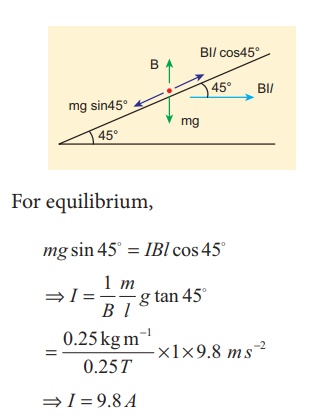
For equilibrium,
mg sin 45┬║ = IBl cos 45 ┬║
ŌćÆ I = I/B m/l g tan 45 ┬║
ŌćÆ I = 9.8 A
So, we need to supply current of 9.8 A to keep the metallic rod stationary.
Related Topics