Explanation, Formulas, Solved Example Problems - CoulombŌĆÖs Inverse Square Law of Magnetism | 12th Physics : Magnetism and Magnetic Effects of Electric Current
Chapter: 12th Physics : Magnetism and Magnetic Effects of Electric Current
CoulombŌĆÖs Inverse Square Law of Magnetism
COULOMBŌĆÖS INVERSE SQUARE LAW OF MAGNETISM
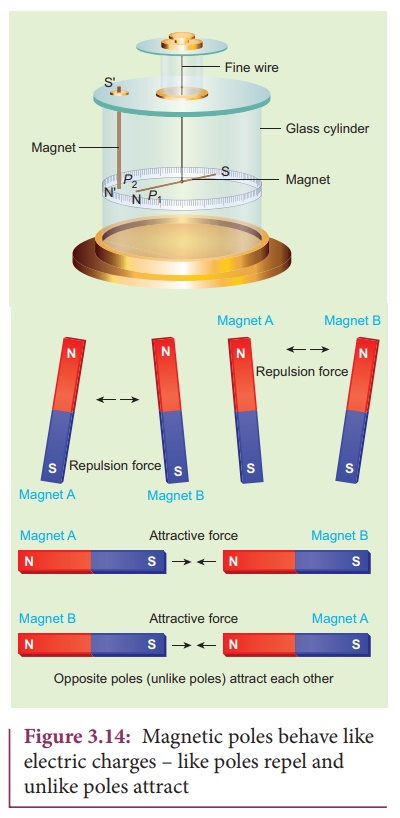
Consider two bar magnets
A and B as shown in Figure 3.14.
When the north pole of
magnet A and the north pole of magnet B or the south pole of magnet A and the
south pole of magnet B are brought closer, they repel each other. On the other
hand, when the north pole of magnet A and the south pole of magnet B or the
south pole of magnet A and the north pole of magnet B are brought closer, their
poles attract each other. This looks similar to CoulombŌĆÖs law for static
charges studied
in Unit I (opposite
charges attract and like charges repel each other). So analogous to CoulombŌĆÖs
law in electrostatics, (Refer unit we can state CoulombŌĆÖs law for magnetism
(Figure 3.15) as follows:

The force of attraction
or repulsion between two magnetic poles is directly proportional to the product
of their pole strengths and inversely proportional to the square of the distance
between them.
Mathematically, we can
write
where mA and
mB are pole strengths of two poles and r is the distance
between two magnetic poles.

where k is a
proportionality constant whose value depends on the surrounding medium. In S.I.
unit, the value of k for free space is
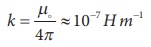
where ╬╝o is
the absolute permeability of free space (air or vacuum).
EXAMPLE 3.5
The repulsive force
between two magnetic poles in air is 9 x 10-3 N. If the two poles
are equal in strength and are separated by a distance of 10 cm, calculate the
pole strength of each pole.
Solution:
The force between two
poles are given by

The magnitude of the
force is
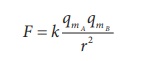
Given :ŌĆé F = 9 x 10-3N,
r = 10 cm = 10 x 10-2 m
Therefore,
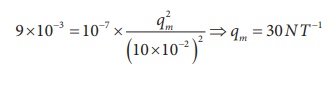
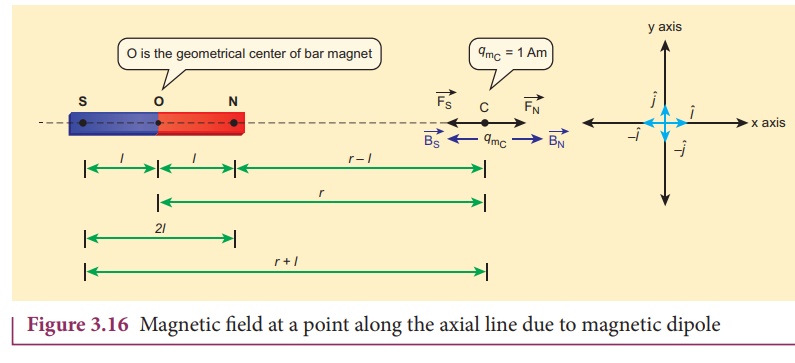
1. Magnetic field at a point along the axial line of the magnetic dipole (bar magnet)
Consider a bar magnet NS
as shown in Figure 3.16. Let N be the North Pole and S be the south pole of the
bar magnet, each of pole strength qm and separated by a distance of
2l. The magnetic field at a point C (lies along the axis of the magnet)
at a distance from the geometrical center O of the bar magnet can be computed
by keeping unit
north pole (qmc = 1 A m) at C. The force
experienced by the unit north pole at Cdue to pole strength can be computed
using CoulombŌĆÖs law of magnetism as follows:
The force of repulsion
between north pole of the bar magnet and unit north pole at point C (in free
space) is

where r ŌĆō l is the distance between north pole of the bar magnet and unit north pole at C.
The force of attraction
between South Pole of the bar magnet and unit North Pole at point C (in free
space) is
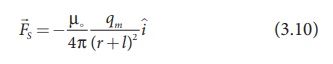
where r + l is
the distance between south pole of the bar magnet and unit north pole at C.
From equation (3.9) and
(3.10), the net force at point C is  . From definition, this
net force is the magnetic field due to magnetic dipole at a point C (
. From definition, this
net force is the magnetic field due to magnetic dipole at a point C ( ![]() =
=![]() )
)
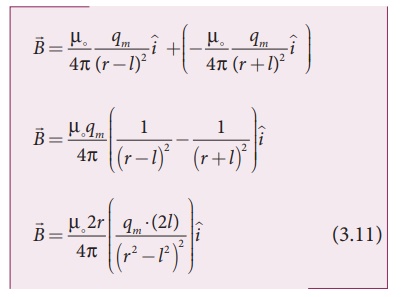
Since, magnitude of
magnetic dipole moment is 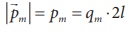 the magnetic field at a point C
equation (3.11) can be written as
the magnetic field at a point C
equation (3.11) can be written as

If the distance between
two poles in a bar magnet are small (looks like short magnet) compared to the distance
between geometrical centre O of bar magnet and the location of point C i.e., r
>>l then,

Therefore,
using equation (3.13) in equation (3.12), we get

2. Magnetic field at a point along the equatorial line due to a magnetic dipole (bar magnet)
Consider a bar magnet NS
as shown in Figure 3.17. Let N be the north pole and S be the south pole of the
bar magnet, each with pole strength q m and separated by a distance
of 2l. The magnetic field at a point C (lies along the equatorial line)
at a distance r from the geometrical center O of the bar magnet can be
computed by keeping unit north pole (qmC = 1 A m) at C. The force
experienced by the unit north pole at C due to pole strength N-S can be
computed using CoulombŌĆÖs law of magnetism as follows:
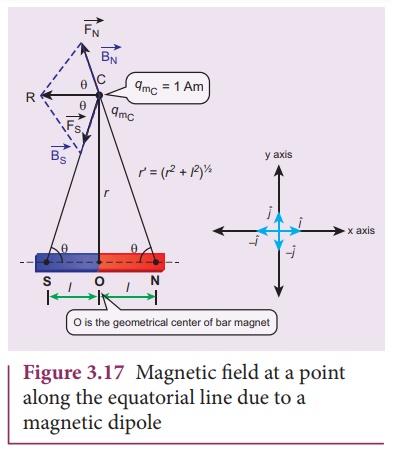
The force of repulsion
between North Pole of the bar magnet and unit north pole at point C (in free
space) is

The force of attraction
(in free space) between south pole of the bar magnet and unit north pole at
point C is (Figure 3.18) is
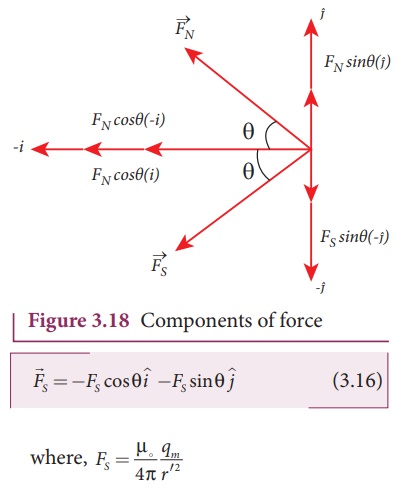
From equation
(3.15) and equation (3.16),
the net force at point C is  . This net force is equal to the
magnetic field at the point C.
. This net force is equal to the
magnetic field at the point C.

In a right angle
triangle NOC as shown in the Figure 3.17

Substituting equation
(3.18) in equation (3.17) we get

Since, magnitude of
magnetic dipole moment is |![]() m| = pm = qm 2l and substituting in
equation (3.19), the magnetic field at a point C is
m| = pm = qm 2l and substituting in
equation (3.19), the magnetic field at a point C is
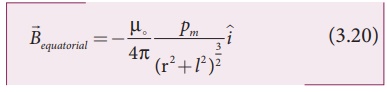
If the distance between
two poles in a bar magnet are small (looks like short magnet) when compared to
the distance between geometrical center O of bar magnet and the location of
point C i.e., r >>l, then,

Therefore, using
equation (3.21) in equation (3.20), we get

Since 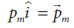 , In
general, the magnetic, field at equatorial point is given by
, In
general, the magnetic, field at equatorial point is given by
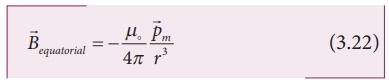
Note that magnitude of B
axial is twice that of magnitude of Bequatorial and the
direction of Baxial and Bequatorial are opposite.
EXAMPLE 3.6
A short bar magnet has a
magnetic moment of 0.5 J T-1. Calculate magnitude and direction of
the magnetic field produced by the bar magnet which is kept at a distance of
0.1 m from the center of the bar magnet along (a) axial line of the bar magnet
and (b) normal bisector of the bar magnet.
Solution
Given magnetic moment
0.5 J T-1 and distance r = 0.1 m
(a) When the point lies
on the axial line of the bar magnet, the magnetic field for short magnet is
given by
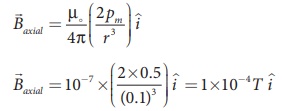
Hence, the magnitude of
the magnetic field along axial is Baxial = 1 x 10-4 T and
direction is towards South to North.
(b) When the point lies
on the normal bisector (equatorial) line of the bar magnet, the magnetic field
for short magnet is given by

Hence, the magnitude of
the magnetic field along axial is Bequatorial = 0.5 x 10-4
T and direction is towards North to South.
Note that magnitude of Baxial
is twice that of magnitude of Bequatorial and the direction of Baxial
and Bequatorial are opposite.
Related Topics