Chapter: 12th Physics : Magnetism and Magnetic Effects of Electric Current
Ampere’s Circuital Law
AMPERE’S CIRCUITAL LAW
Ampère’s circuital law
is used to calculate magnetic field at a point whenever there is a symmetry in
the problem. This is similar to Gauss’s law in electrostatics. These are
powerful methods whenever there is symmetry in the problem.
1. Definition and explanation of Ampère’s circuital law
Ampère’s law: The line integral of magnetic
field over a closed loop is μ0 times net current enclosed by the
loop.
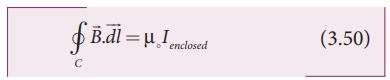
where Ienclosed
is the net current linked by the closed loop C. Note that the line integral
does not depend on the shape of the path or the position of the conductor with
the magnetic field.
2. Magnetic field due to the current carrying wire of infinite length using Ampère’s law
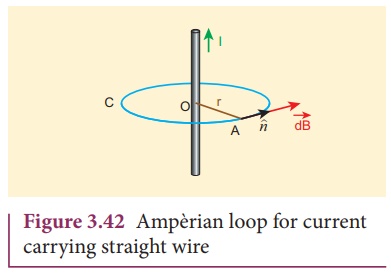
Consider a straight
conductor of infinite length carrying current I and the direction ofmagnetic
field lines is shown in Figure 3.42. Since the wire is geometrically
cylindrical in shape and symmetrical about its axis, we construct an Ampèrian
loop in the form of a circular shape at a distance r from the centre of
the conductor as shown in Figure 3.42. From the Ampère’s law, we get
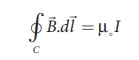
where 
is the line element along the amperian loop (tangent to the circular loop).
Hence, the angle between magnetic field vector and line element is zero.
Therefore,
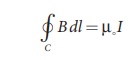
where I is the current
enclosed by the Ampèrian loop. Due to the symmetry, the magnitude of the
magnetic field is uniform over the Ampèrian loop, we can take B out of the
integration.
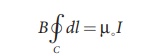
For a circular loop, the
circumference is 2Ï€r, which implies,
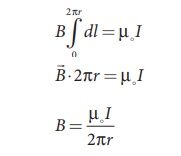
In vector form, the
magnetic field is
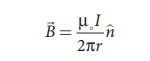
where n is the
unit vector along the tangent to the Ampèrian loop as shown in the Figure 3.42.
This perfectly agrees with the result obtained from Biot-Savart’s law as given
in equation (3.39).
EXAMPLE 3.18
Compute the magnitude of
the magnetic field of a long, straight wire carrying a current of 1A at
distance of 1m from it. Compare it with Earth’s magnetic field.
Solution
Given that 1 = 1 A and
radius r = 1 m
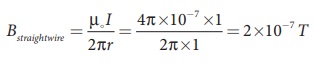
But the Earth’s magnetic
field is BEarth ≈ 10−5
T
So, Bstraightwire
is one hundred times smaller than BEarth.
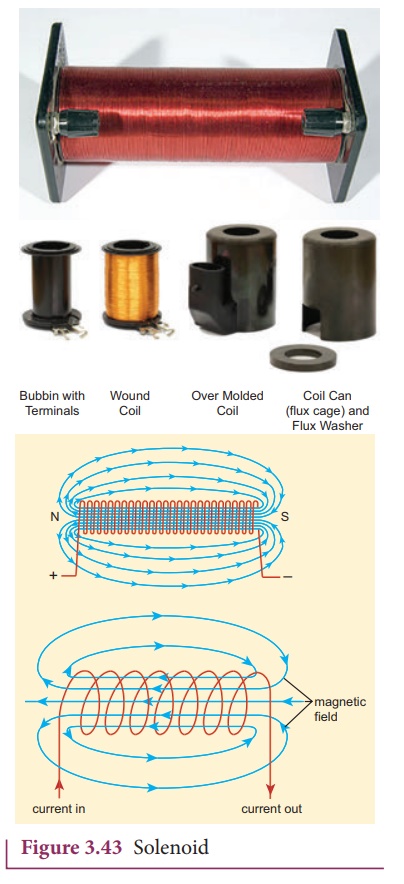
3. Solenoid
A solenoid is a long
coil of wire closely wound in the form of helix as shown in Figure 3.43. When
electric current is passed through the solenoid, the magnetic field is
produced. The magnetic field of the solenoid is due to the superposition of
magnetic fields of each turn of the solenoid. The direction of magnetic field
due to solenoid is given by right hand palm-rule (mnemonic).
Inside the solenoid, the
magnetic field is nearly uniform and parallel to its axis whereas, outside the
solenoid the field is negligibly small. Based on the direction of the current,
one end of the solenoid behaves like North Pole and the other end behaves like
South Pole.
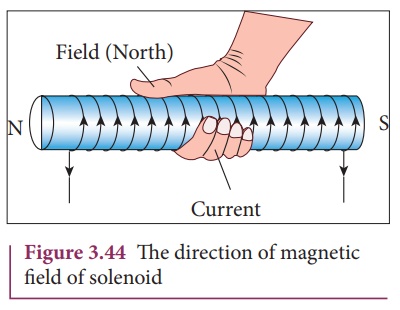
The current carrying
solenoid is held in right hand. If the fingers curl in the direction of
current, then extended thumb gives the direction of magnetic field of current
carrying solenoid. It is shown in Figure 3.44. Hence, the magnetic field of a
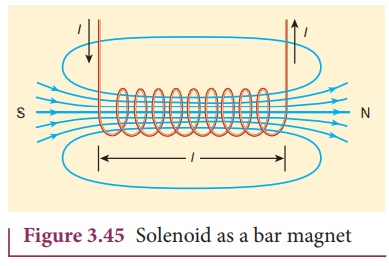
The solenoid is assumed
to be long which means that the length of the solenoid is large when compared
to its diameter. The winding need not to be always circular, it can also be in
other shapes. We consider here only circularly wound solenoid as shown in
Figure 3.45.
4. Magnetic field due to a long current carrying solenoid
Consider a solenoid of
length L having N turns. The diametre of the solenoid is assumed to be much smaller
when compared to its length and the coil is wound very closely.
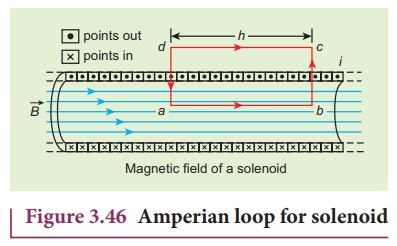
In order to calculate
the magnetic field at any point inside the solenoid, we use Ampere’s circuital
law. Consider a rectangular loop abcd as shown in Figure 3.46. Then from Ampère’s
circuital law,
The left hand side of
the equation is
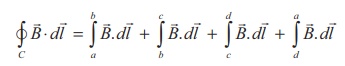
Since the elemental
lengths along bc and da are perpendicular to the magnetic field which is along
the axis of the solenoid, the integrals
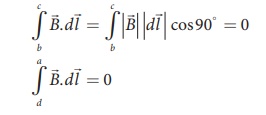
Since the magnetic field
outside the solenoid is zero, the integral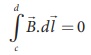 
For the path along ab,
the integral is
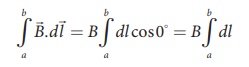
where the length of the
loop ab as shown in the Figure 3.46 is h. But the choice of length of the loop
ab is arbitrary. We can take very large loop such that it is equal to the
length of the solenoid L. Therefore the integral is
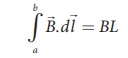
Let N I be the current
passing through the solenoid of N turns, then
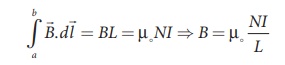
The number of turns per
unit length is given by N/L =
n, Then
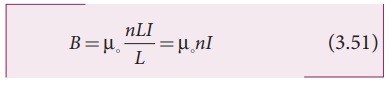
Since n is a
constant for a given solenoid and μ0 is also constant. For a fixed
current I, the magnetic field inside the solenoid is also a constant.
EXAMPLE 3.19
Calculate the magnetic
field inside a solenoid, when
(a) the length of the
solenoid becomes twice and fixed number of turns
(b) both the length of
the solenoid and number of turns are double
(c) the number of turns
becomes twice for the fixed length of the solenoid
Compare the results.
Solution
The magnetic field of a
solenoid (inside) is
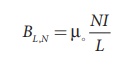
(a) length of the
solenoid becomes twice and fixed number of turns
L→2L (length becomes
twice)
N→N (number of turns are
fixed)
The magnetic field is
B2L , N = µ
NI/2L = 1/2 BL ,N
(b) both the length of
the solenoid and number of turns are double
L→2L (length becomes
twice)
N→2N (number of turns
becomes twice)
The magnetic field is
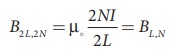
(c) the number of turns
becomes twice but for the fixed length of the solenoid
L→L (length is fixed)
N→2N (number of turns
becomes twice)
The magnetic field is
BL ,2 N = µ,
2NI/L = 2BL ,N
From the above results,
BL ,2 N >
B2 L ,2 N > B2 L , N
Thus, strength of the magnetic field is increased when we pack more loops into the same length for a given current.
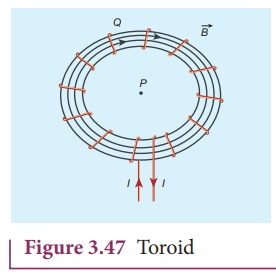
5. Toroid
A solenoid is bent in
such a way its ends are joined together to form a closed ring shape, is called
a toroid which is shown in Figure 3.47. The magnetic field has constant
magnitude inside the toroid whereas in the interior region (say, at point P)
and exterior region (say, at point Q), the magnetic field is zero.
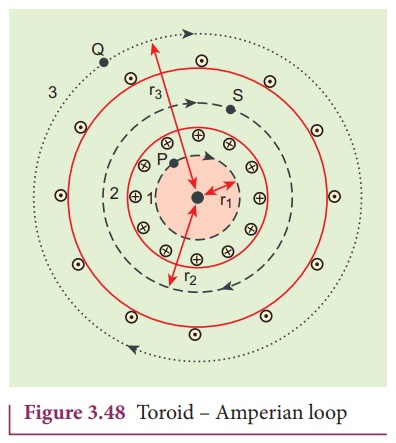
(a) Open space interior to the toroid
Let us calculate the
magnetic field BP at point P. We construct an Amperian loop 1 of
radius r1 around the point P as shown in Figure 3.48. For
simplicity, we take circular loop so that the length of the loop is its circumference.
L1 = 2Ï€r1
Ampère’s circuital law
for the loop 1 is
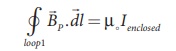
Since, the loop1
encloses no current, Ienclosed = 0
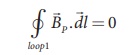
This is possible only if
the magnetic field at point P vanishes i.e.
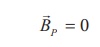
(b) Open space exterior to the toroid
Let us calculate the
magnetic field BQ at point Q. We construct an Amperian loop 3 of
radius r3 around the point Q as shown in Figure 3.48. The length of
the loop is
L3 = 2Ï€r3
Ampère’s circuital law
for the loop 3 is
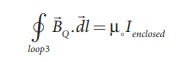
Since, in each turn of
the toroid loop, current coming out of the plane of paper is cancelled by the
current going into the plane of paper. Thus, Ienclosed = 0
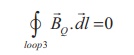
This is possible only if
the magnetic field at point Q vanishes i.e.
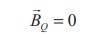
(c) Inside the toroid
Let us calculate the
magnetic field BS at point S by constructing an Amperian loop 2 of
radius r2 around the point S as shown in Figure 3.48. The length of
the loop is
L2 = 2Ï€r2
Ampere’s circuital law
for the loop 2 is
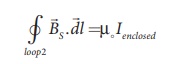
Let I be the current
passing through the toroid and N be the number of turns of the toroid, then
The number of turns per unit length
is n = N/2Ï€r2 , then the magnetic field at point S is
Related Topics