Vector triple product

Vector triple product

Definition 6.5

For a given set of three vectors  , ,  , the vector Ã—( Ã— ) is called a  vector triple product.

Note

Given any three vectors , , the following are vector triple products :

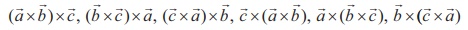
Using the well known properties of the vector product, we get the following theorem.

Theorem 6.7

The vector triple product satisfies the following properties.

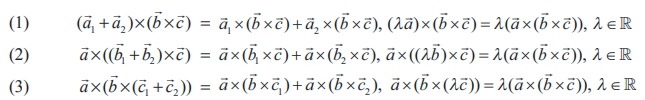
Remark

Vector triple product is not associative. This means that 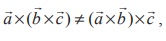 for some vectors , , .

Justification

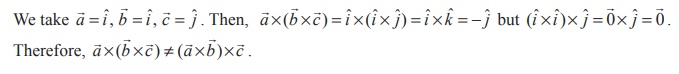
The following theorem gives a simple formula to evaluate the vector triple product.

Theorem 6.8 (Vector Triple product expansion)

For any three vectors , ,  we have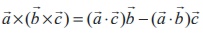 

Proof

Let us choose the coordinate axes as follows :

Let x -axis be chosen along the line of action of , y -axis be chosen in the plane passing through  and parallel to  , and z -axis be chosen perpendicular to the plane containing  and . Then, we have

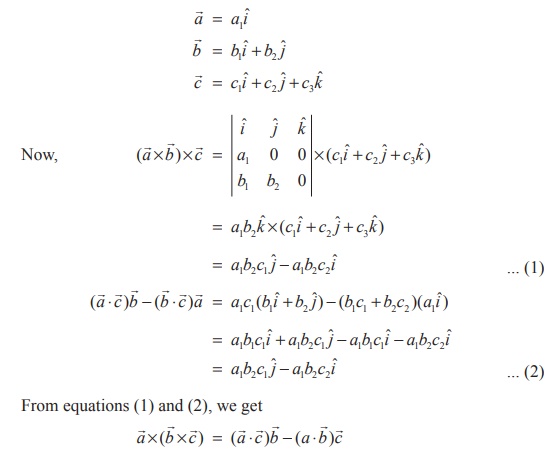
Note

(3) In ( Ã— ) ×c , consider the vectors inside the brackets, call  as the middle vector and  as the non-middle vector. Similarly, in 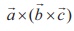, is the middle vector and  is the non-middle vector. Then we observe that a vector triple product of these vectors is equal to

λ (middle vector) −µ (non-middle vector)

 where λ is the dot product of the vectors other than the middle vector and μ is the dot

product of the vectors other than the non-middle vector.