Meeting Point of a Line and a Plane

Meeting Point of a Line and a Plane

Theorem 6.23

The position vector of the point of intersection of the straight line  and the plane

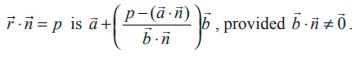
Proof

Let  be the equation of the given line which is not parallel to the given plane whose equation is 

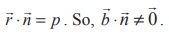
Let  be the position vector of the meeting point of the line with the plane. Then  satisfies both  and  â‹… = p for some value of t , say t₁. So, We get

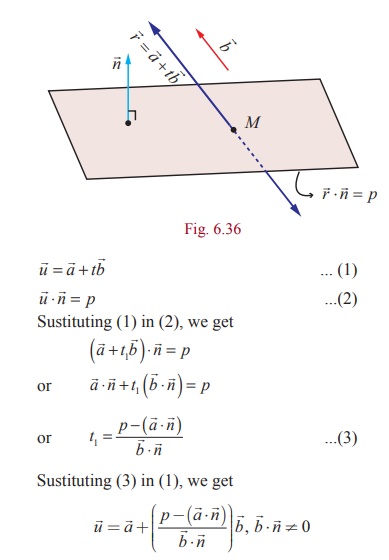
Example 6.56

Find the coordinates of the point where the straight line 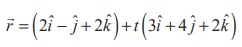 intersects the plane x − y + z − 5 = 0 .

Solution

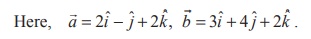
The vector form of the given plane is 

We know that the position vector of the point of intersection of the line  and the plane

Therefore,the position vector of the point of intersection of the given line and the given plane is

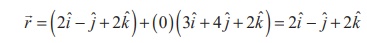
That is, the given straight line intersects the plane at the point (2, −1, 2 ).

Aliter

The Cartesian equation of the given straight line is 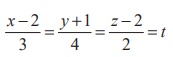(say)

We know that any point on the given straight line is of the form (3t + 2,4 t-1,2t+ 2) . If the given line and the plane intersects, then this point lies on the given pane x-y+z-5=0.

So, (3t + 2) - (4t-1) + (2t+ 2) - 5 = 0 ⇒ t = 0.

Therefore, the given line intersects the given plane at the point  (2,-1, 2)