Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Equation of a plane passing through two given distinct points and is parallel to a non-zero vector
Equation of a plane passing through two given distinct points and is parallel
to a non-zero vector
(a) Parametric form of vector equation
The parametric form of vector equation of the plane passing
through two given distinct points A and B with position vectors ![]() and
and ![]() , and parallel to a non-zero vector
, and parallel to a non-zero vector ![]() is
is

(b) Non-parametric form of vector equation
Equation (1) can be written equivalently in non-parametric
vector form as
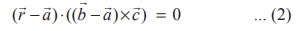
Where ( ![]() -
- ![]() ) and
) and ![]() are not parallel vectors.
are not parallel vectors.
(c) Cartesian form of equation
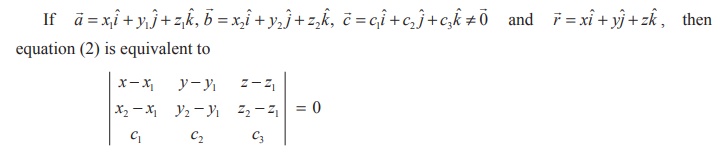
This is the required Cartesian equation of the plane.
Example 6.43
Find the non-parametric form of vector equation, and Cartesian
equation of the plane passing through the point (0,1, −5) and parallel to the
straight lines 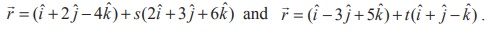
Solution
We observe that the required plane is parallel to the
vectors 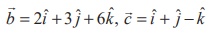 and passing through the point (0,1, −5) with position vector
and passing through the point (0,1, −5) with position vector ![]() .
.
We observe that ![]() is not parallel to
is not parallel to ![]() .
Then the vector equation of the plane in non-parametric form is given by
.
Then the vector equation of the plane in non-parametric form is given by 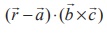 = 0. …(1)
= 0. …(1)
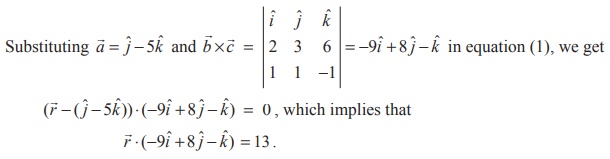
If ![]() = xˆi + yˆj + zˆk is the position vector of an arbitrary point on the plane, then
from the above equation, we get the Cartesian equation of the plane as -9x + 8
y - z = 13 or 9x - 8 y + z +13 = 0 .
= xˆi + yˆj + zˆk is the position vector of an arbitrary point on the plane, then
from the above equation, we get the Cartesian equation of the plane as -9x + 8
y - z = 13 or 9x - 8 y + z +13 = 0 .
Example 6.44
Find the vector parametric, vector non-parametric and Cartesian
form of the equation of the plane passing through the points (−1, 2, 0), (2, 2
−1) and parallel to the straight line
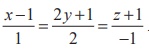
Solution
The required plane is parallel to the given line and so it is
parallel to the vector ![]() = iˆ + ˆj − ˆk and
he plane passes through the points
= iˆ + ˆj − ˆk and
he plane passes through the points ![]() = −ˆi + 2ˆj,
= −ˆi + 2ˆj, ![]() = 2ˆi + 2ˆj − ˆk .
= 2ˆi + 2ˆj − ˆk .
vector equation of the plane in parametric form is 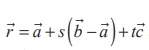 , where
s, t ∈ R which implies that
, where
s, t ∈ R which implies that 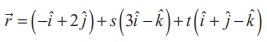 = (-ˆi + 2ˆj ) + s (3ˆi - ˆk )+ t (ˆi + ˆj - ˆk ) , where s, t ∈ R.
= (-ˆi + 2ˆj ) + s (3ˆi - ˆk )+ t (ˆi + ˆj - ˆk ) , where s, t ∈ R.
vector equation of the plane in non-parametric form is 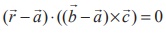
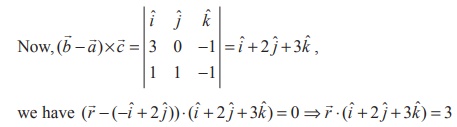
we have (![]() - (-iˆ + 2ˆ j)) . (ˆi + 2ˆj + 3ˆk ) = 0 ⇒
- (-iˆ + 2ˆ j)) . (ˆi + 2ˆj + 3ˆk ) = 0 ⇒ ![]() . (ˆi + 2ˆ j + 3ˆk ) = 3
. (ˆi + 2ˆ j + 3ˆk ) = 3
If ![]() = xˆi + yˆj + zˆk is the position vector of an arbitrary point on the plane, then
from the above equation, we get the Cartesian equation of the plane as x + 2 y
+ 3z = 3 .
= xˆi + yˆj + zˆk is the position vector of an arbitrary point on the plane, then
from the above equation, we get the Cartesian equation of the plane as x + 2 y
+ 3z = 3 .
Related Topics