Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Angle between a line and a plane
Angle
between a line and a plane
We know that the angle between a line and a plane is the complement of the
angle between the normal to the plane and the line
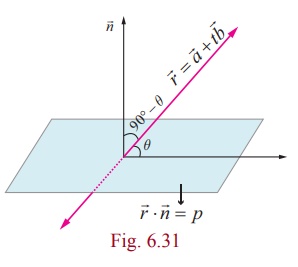
Let ![]() =
= ![]() + t
+ t![]() be the equation of the line and
be the equation of the line and ![]() ⋅
⋅ ![]() = p be the equation of the plane. We know that
= p be the equation of the plane. We know that ![]() is
parallel to the given line and
is
parallel to the given line and ![]() is normal to the given plane.
If θ is the acute angle between the line and the plane, then the acute
angle between
is normal to the given plane.
If θ is the acute angle between the line and the plane, then the acute
angle between ![]() and
and ![]() is ((π/2)-θ).Therefore,
is ((π/2)-θ).Therefore,
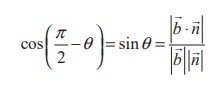
So, the acute angle between the line and the plane is given by θ
= 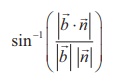 ….(1)
….(1)
In Cartesian form if 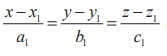 and ax + by + cz = p
are the equations of the line and the plane, then
and ax + by + cz = p
are the equations of the line and the plane, then ![]() = a1iˆ + b1 ˆj + c1kˆ and
= a1iˆ + b1 ˆj + c1kˆ and ![]() = aˆi
+ bˆj + cˆk . Therefore, using (1), the acute angle θ between the line and
plane is given by
= aˆi
+ bˆj + cˆk . Therefore, using (1), the acute angle θ between the line and
plane is given by
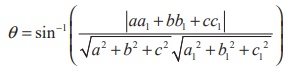
Remark
(i) If the line is perpendicular to the plane, then the line is
parallel to the normal to the plane.
So, ![]() is perpendicular to
is perpendicular to ![]() . Then we have
. Then we have ![]() = λ
= λ![]() . λ ∈ R ,which gives
. λ ∈ R ,which gives 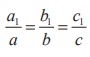
(ii) If the line is parallel to the plane, then the line is
perpendicular to the normal to the plane.
Therefore, ![]() .
.![]() = 0 ⇒ aa1 + bb1
+ cc1 = 0
= 0 ⇒ aa1 + bb1
+ cc1 = 0
Example 6.48
Find the angle between the straight line ![]() = (2ˆi + 3ˆj + ˆk )+ t (ˆi
- ˆj + ˆk ) and the plane 2x - y + z = 5 .
= (2ˆi + 3ˆj + ˆk )+ t (ˆi
- ˆj + ˆk ) and the plane 2x - y + z = 5 .
Solution
The angle between a line ![]() =
= ![]() + t
+ t![]() and a plane
and a plane ![]() ⋅
⋅ ![]() = p with normal
= p with normal ![]() is θ
is θ
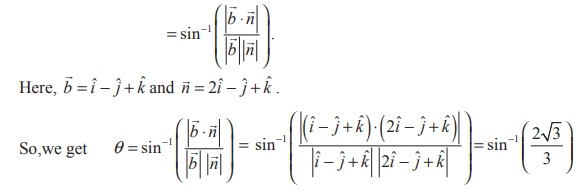
Related Topics