Equation of a plane passing through the line of intersection of two given planes

Equation of a plane passing through the line of intersection of two given planes

Theorem 6.22

The vector equation of a plane which passes through the line of intersection of the planes

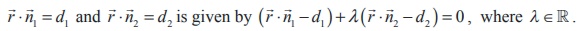
Proof

Consider the equation

The equation (3) represents a plane. Hence (1) represents a plane.

Let ₁ be the position vector of any point on the line of intersection of the plane. Then  1 satisfies both the equations  â‹… 1  = d1  and  â‹… 2  = d2  . So, we have

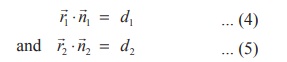
By (4) and (5),  1 satisfies (1). So, any point on the line of intersection lies on the plane (1). This proves that the plane (1) passes through the line of intersection.

The cartesian equation of a plane which passes through the line of intersection of the planes a₁ x + b₁y + c₁z = d₁ and a₂x + b₂y + c₂z = d₂ is given by

( a1 x + b1y + c1z = d1) Î» (  a2x + b2y + c2z = d2) = 0

Example 6.53

Find the equation of the plane passing through the intersection of the planes  â‹… (i + j + k )+1 = 0 and  â‹… (2i - 3j + 5k ) = 2 and the point (−1, 2,1) .

Solution

We know that the vector equation of a plane passing through the line of intersection of the planes

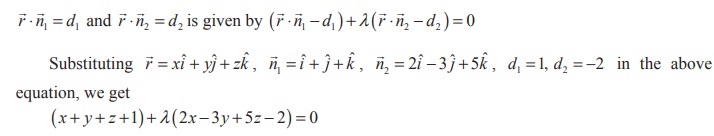
Since this plane passes through the point (−1, 2,1) , we get λ =3/5 , and hence the required equation of the plane is 11x − 4 y + 20z = 1 .

Example 6.54

Find the equation of the plane passing through the intersection of the planes 2x + 3y − z + 7 = 0 and x + y − 2z + 5 = 0 and is perpendicular to the plane x + y − 3z − 5 = 0 .

Solution

The equation of the plane passing through the intersection of the planes 2x + 3y − z + 7 = 0 and x + y − 2z + 5 = 0 is (2x + 3y − z + 7) + λ ( x + y − 2z + 5) = 0 or

(2 + λ ) x + (3 + λ ) y + (−1− 2λ ) z + (7 + 5λ ) = 0

since this plane is perpendicular to the given plane x + y − 3z − 5 = 0 , the normals of these two planes are perpendicular to each other. Therefore, we have

(1)(2 + λ ) + (1)(3 + λ ) + (−3)(−1− 2λ ) z = 0

which implies that λ = −1 .Thus the required equation of the plane is

(2x + 3y − z + 7) − ( x + y − 2z + 5) = 0 ⇒ x + 2 y + z + 2 = 0 .