Definition, Properties, Theorem, Proof, Solved Example Problems, Solution - Scalar triple product | 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Scalar triple product
Scalar triple product
Definition 6.4
For a given set of three vectors ![]() ,
, ![]() , and
, and ![]() , the scalar (
, the scalar (![]() ×
× ![]() ) ⋅
) ⋅ ![]() is called a scalar triple product of
is called a scalar triple product of ![]() ,
, ![]() ,
, ![]() .
.
Remark

Note
Given any three vectors ![]() ,
, ![]() ,
, ![]() and c the following are scalar triple products:
and c the following are scalar triple products:
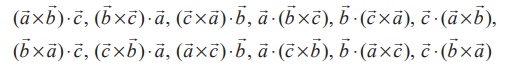
Geometrical interpretation of scalar triple product
Geometrically, the absolute value of the scalar triple product ( ![]() ×
× ![]() ) .
) .![]() . is the volume of the parallelepiped formed by using the three vectors
. is the volume of the parallelepiped formed by using the three vectors ![]() ,
, ![]() and
and ![]() as co-terminus edges. Indeed, the magnitude of the vector (
as co-terminus edges. Indeed, the magnitude of the vector (![]() ×
× ![]() ) is the area of the parallelogram formed by using
) is the area of the parallelogram formed by using ![]() and
and ![]() ; and the direction of the vector (
; and the direction of the vector (![]() ×
× ![]() ) is perpendicular to the plane parallel to both
) is perpendicular to the plane parallel to both ![]() and
and ![]() .
.
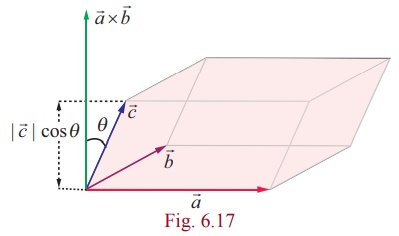
Therefore, | (![]() ×
× ![]() ) ⋅
) ⋅ ![]() | is |
| is | ![]() ×
× ![]() ||
|| ![]() || cosθ | , where θ is the angle between
|| cosθ | , where θ is the angle between ![]() ×
× ![]() and . From Fig. 6.17, we observe that |
and . From Fig. 6.17, we observe that | ![]() | | cosθ | is the height of the parallelepiped formed by using the three vectors as adjacent vectors. Thus, | (
| | cosθ | is the height of the parallelepiped formed by using the three vectors as adjacent vectors. Thus, | (![]() ×
× ![]() ) ⋅
) ⋅ ![]() | is the volume of the parallelepiped.
| is the volume of the parallelepiped.
The following theorem is useful for computing scalar triple products.
Theorem 6.1
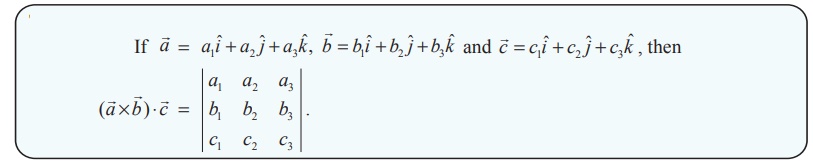
Proof
By definition, we have
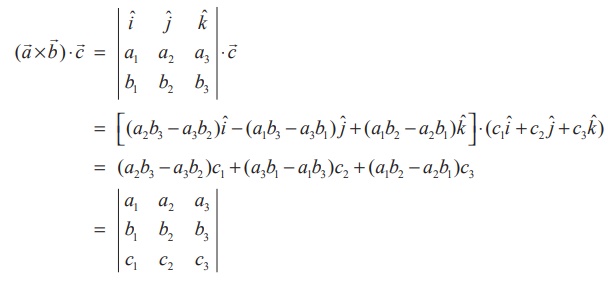
which completes the proof of the theorem.
Properties of the scalar triple product
Theorem 6.2
For any three vectors ![]() ,
, ![]() and
and ![]() , (
, (![]() ×
× ![]() ) ⋅
) ⋅ ![]() =
= ![]() ⋅ (
⋅ (![]() ×
× ![]() ) .
) .
Proof
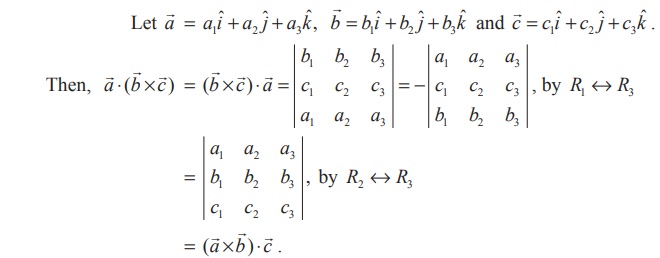
Hence the theorem is proved.
Note
By Theorem 6.2, it follows that, in a scalar triple product, dot and cross can be interchanged without altering the order of occurrences of the vectors, by placing the parentheses in such a way that dot lies outside the parentheses, and cross lies between the vectors inside the parentheses. For instance, we have

Notation
For any three vectors ![]() ,
, ![]() and
and ![]() , the scalar triple product (
, the scalar triple product (![]() ×
× ![]() ) ⋅
) ⋅ ![]() is denoted by [
is denoted by [![]() ×
× ![]() ,
, ![]() ] . [
] . [![]() ×
× ![]() ,
, ![]() ] is read as box a, b, c . For this reason and also because the absolute value of a scalar triple product represents the volume of a box (rectangular parallelepiped),a scalar triple product is also called a box product.
] is read as box a, b, c . For this reason and also because the absolute value of a scalar triple product represents the volume of a box (rectangular parallelepiped),a scalar triple product is also called a box product.
Note
(1) 
In other words, [![]() ,
, ![]() ,
, ![]() ] = [
] = [![]() ,
, ![]() ,
, ![]() ] = [
] = [![]() ,
, ![]() ,
, ![]() ] ; that is, if the three vectors are permuted in the same cyclic order, the value of the scalar triple product remains the same.
] ; that is, if the three vectors are permuted in the same cyclic order, the value of the scalar triple product remains the same.
(2) If any two vectors are interchanged in their position in a scalar triple product, then the value of the scalar triple product is (-1) times the original value. More explicitly,
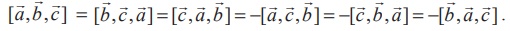
Theorem 6.3
The scalar triple product preserves addition and scalar multiplication. That is,
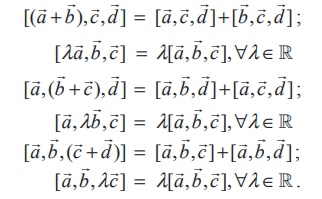
Proof
Using the properties of scalar product and vector product, we get
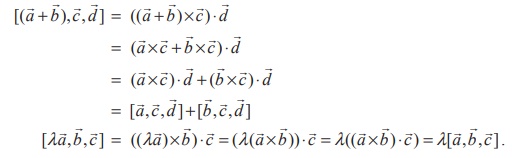
Using the first statement of this result, we get the following.
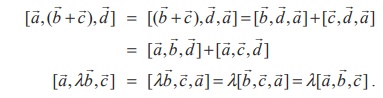
Similarly, the remaining equalities are proved.
We have studied about coplanar vectors in XI standard as three nonzero vectors of which, one can be expressed as a linear combination of the other two. Now we use scalar triple product for the characterisation of coplanar vectors.
Theorem 6.4
The scalar triple product of three non-zero vectors is zero if, and only if, the three vectors are coplanar.
Proof
Let ![]() ,
, ![]() ,
, ![]() be any three non-zero vectors. Then,
be any three non-zero vectors. Then,
![]() ×
× ![]() ⋅
⋅ ![]() = 0 ⇔
= 0 ⇔ ![]() is perpendicular to
is perpendicular to ![]() ×
× ![]()
⇔ ![]() lies in the plane which is parallel to both
lies in the plane which is parallel to both ![]() and
and ![]()
![]() ,
, ![]() ,
, ![]() are coplanar.
are coplanar.
Theorem 6.5
Three vectors ![]() ,
, ![]() ,
, ![]() are coplanar if, and only if, there exist scalars r, s, t ∈ R such that atleast one of them is non-zero and r
are coplanar if, and only if, there exist scalars r, s, t ∈ R such that atleast one of them is non-zero and r![]() + s
+ s![]() + t
+ t![]() =
= ![]() .
.
Proof
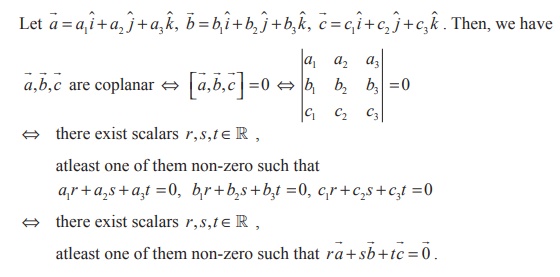
Theorem 6.6

Proof
Applying the distributive law of cross product and using
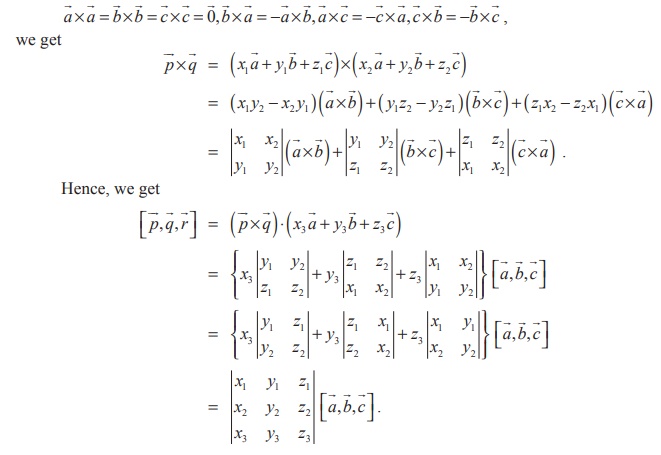
Note
By theorem 6.6, if ![]() ,
,![]() ,
, ![]() are non-coplanar and
are non-coplanar and
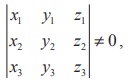
then the three vectors  are also non-coplanar.
are also non-coplanar.
Example 6.12
If ![]() = −3iˆ− ˆj + 5ˆk,
= −3iˆ− ˆj + 5ˆk, ![]() = ˆi − 2 ˆj + k,
= ˆi − 2 ˆj + k, ![]() = 4 ˆj − 5ˆk , find
= 4 ˆj − 5ˆk , find ![]() ⋅ (
⋅ (![]() ×
× ![]() ) .
) .
Solution:
By the defination of scalar triple product of three vectors,
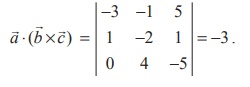 , the volume of the parallelepiped is | −7 | 7 = cubic units.
, the volume of the parallelepiped is | −7 | 7 = cubic units.
Example 6.13
Find the volume of the parallelepiped whose coterminus edges are given by the vectors 2iˆ − 3 ˆj + 4kˆ, iˆ + 2 ˆj − kˆ and 3iˆ − ˆj + 2kˆ .
Solution
We know that the volume of the parallelepiped whose coterminus edges are ![]() ,
, ![]() , c is given by | [
, c is given by | [![]() ,
, ![]() ,
, ![]() ] | . Here,
] | . Here, ![]() = 2iˆ − 3ˆ j + 4ˆk,
= 2iˆ − 3ˆ j + 4ˆk, ![]() = ˆi + 2 ˆj − ˆk,
= ˆi + 2 ˆj − ˆk, ![]() = 3ˆi − ˆj + 2ˆk.
= 3ˆi − ˆj + 2ˆk.
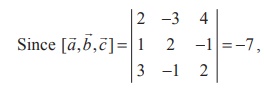
Example 6.14
Show that the vectors iˆ + 2 ˆj − 3kˆ, 2iˆ − ˆj + 2kˆ and 3iˆ + ˆj − kˆ are coplanar.
Solution
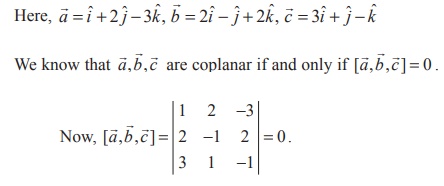
Therefore, the three given vectors are coplanar.
Example 6.15
If 2iˆ − ˆj + 3kˆ, 3iˆ + 2 ˆj + kˆ, iˆ + mˆj + 4kˆ are coplanar, find the value of m .
Solution
Since the given three vectors are coplanar, we have 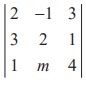 = 0 ⇒ m = -3.
= 0 ⇒ m = -3.
Example 6.16
Show that the four points (6, −7, 0), (16, −19, −4), (0, 3, −6), (2, −5,10) lie on a same plane.
Solution
Let A = (6, −7, 0), B = (16, −19, −4), C = (0, 3, −6), D = (2, −5,10) . To show that the four points A, B, C, D lie on a plane, we have to prove that the three vectors ![]() ,
,![]() ,
, ![]() are coplanar.
are coplanar.
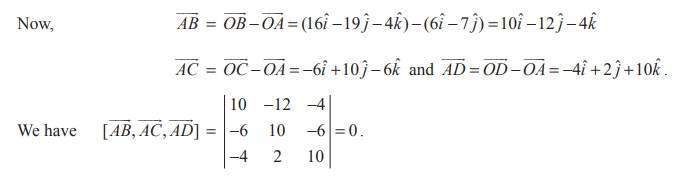
Therefore, the three vectors ![]() ,
,![]() ,
, ![]() , are coplanar and hence the four points A, B, C, and D lie on a plane.
, are coplanar and hence the four points A, B, C, and D lie on a plane.
Example 6.17
If the vectors ![]() ,
, ![]() ,
, ![]() are coplanar, then prove that the vectors
are coplanar, then prove that the vectors 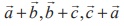 are also coplanar.
are also coplanar.
Solution
Since the vectors ![]() ,
, ![]() ,
, ![]() are coplanar, we have [
are coplanar, we have [![]() ,
, ![]() ,
, ![]() ] = 0. Using the properties of the scalar triple product, we get
] = 0. Using the properties of the scalar triple product, we get
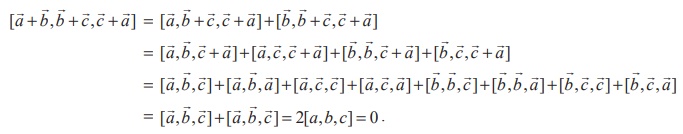
Hence the vectors 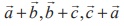 are coplanar.
are coplanar.
Example 6.18
If ![]() ,
, ![]() ,
, ![]() are three vectors, prove that
are three vectors, prove that 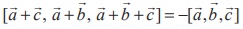 .
.
Solution
Using theorem 6.6, we get
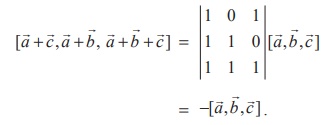
Related Topics