Straight Line passing through two given points

Straight Line passing through two given points

(a) Parametric form of vector equation

Theorem 6.12

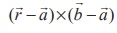The parametric form of vector equation of a line passing through two given points whose position vectors are  and  respectively is , t âˆˆ R.

(b) Non-parametric form of vector equation

The above equation can be written equivalently in non-parametric form of vector equation as

  = 

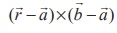(c) Cartesian form of equation

Suppose P is (x, y, z) ,  A is (x1, y1 , z1 ) and B is (x2 , y2 , z2). Then substituting  = x Ë†i + y Ë† j + z Ë†k ,  = x1ˆi + y1ˆ j + z1ˆk and  = x2i + y2 Ë† j +z2ˆk in theorem 6.12 and comparing the coefficients of Ë†i , Ë† j, Ë†k , we get  x âˆ’ x1  = t(x2 âˆ’ x1), y âˆ’ y1  = t( y2 âˆ’ y1), z âˆ’ z1  = t(z2 âˆ’ z1 ) and so the Cartesian equations of a  line passing through two given points (x1, y1, z1) and (x2, y2, z2) are given by

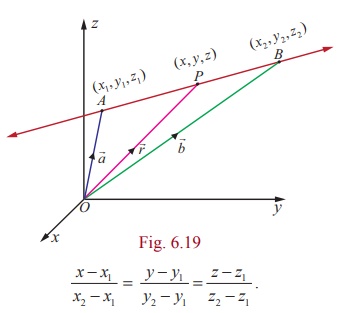
From the above equation, we observe that the direction ratios of a line passing through two given points (x1 , y1 , z1) and (x2 , y2 , z2 ) are given by x2− x1 , y2 âˆ’ y1 , z2 âˆ’ z1, which are also given by any three numbers proportional to them and in particular x1 âˆ’ x2 , y1 âˆ’ y2 , z1 âˆ’ z2.

Example 6.24

A straight line passes through the point (1, 2, −3) and parallel to 4iˆ + 5 ˆj âˆ’ 7kˆ . Find (i) vector equation in parametric form (ii) vector equation in non-parametric form (iii) Cartesian equations of the straight line.

Solution

The required line passes through (1, 2, −3) . So, the position vector of the point is iˆ + 2 ˆj âˆ’ 3kˆ.

Let  = Ë†i + 2 Ë†j âˆ’ 3ˆk and  = 4ˆi + 5 Ë†j âˆ’ 7ˆk . Then, we have

Let a = i + 2 j - 3k and b = 4i + 5 j - 7k . Then, we have

(i) vector equation of the required straight line in parametric form is  =  + t, t âˆˆ R.

Therefore,  = (ˆi + 2 Ë† j - 3 Ë†k ) + t(4 Ë†i + 5 Ë† j - 7 Ë† k ), t∈ R..

(ii)  vector equation of the required straight line in non-parametric form is (  - ) ×  = .

Therefore, (  - (ˆi + 2 Ë†j - 3 Ë†k )) Ã— (4 ˆi + 5 Ë†j - 7 Ë†k ) = .

(iii) Cartesian equations of the required line are (x - x1) / b1 = y - y1 / b1 = (z - z1) / b1.

Here, (x1 , y1 , z1) = (1, 2, -3) and direction ratios of the required line are proportional to 4, 5, -7 . Therefore, Cartesian equations of the straight line are (x -1)/4 = (y â€“ 2)/5 = (z + 3)/-7.

Example 6.25

The vector equation in parametric form of a line is  = (3 ˆi âˆ’ 2 ˆj + 6 ˆk ) + t(2 ˆi âˆ’ ˆj + 3 ˆk ) . Find (i) the direction cosines of the straight line (ii) vector equation in non-parametric form of the line (iii)Cartesian equations of the line.

Solution

Comparing the given equation with equation of a straight line  =  + t , we have = 3 ˆi âˆ’ 2 ˆj + 6 ˆk and  = 2iˆ − ˆj + 3kˆ . Therefore,

(i)   If  = b1iˆ + b2ˆj + b3kˆ ,  then  direction  ratios  of  the  straight  line  are b1 , b2 , b3. Therefore, direction ratios of the given straight line are proportional to 2, -1, 3 , and hence the direction cosines of the given straight line are .

(ii) vector equation of the straight line in non-parametric form is given by  (  -  ) ×  =  . Therefore, (  - (3 ˆi - 2 ˆj + 6 ˆk )) x(2 ˆi - ˆj + 3 ˆk) = 0 .

(iii) Here (x1 , y1 , z1 ) = (3, -2, 6) and the direction ratios are proportional to 2, -1, 3 .

Therefore, Cartesian equations of the straight line are (x – 3)/2 = (y + 2)/-1 = (z – 6)/3

Example 6.26

Find the vector equation in parametric form and Cartesian equations of the line passing through (−4, 2, −3) and is parallel to the line 

Solution

Rewriting the given equations as 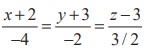 and comparing with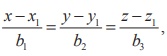 

We have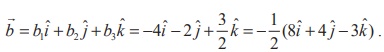 

Clearly,  is parallel to the vector 8iˆ + 4ˆj - 3kˆ . Therefore, a vector equation of the required straight line passing through the given point (-4, 2, -3) and parallel to the vector 8iˆ + 4ˆj - 3kˆ in parametric form is

   = (-4iˆ + 2ˆj  - 3kˆ) + t(8iˆ + 4ˆj - 3kˆ), t âˆˆ R.

Therefore, Cartesian equations of the required straight line are given by

(x + 4) / 8 =  (y – 2) / 4 = (z + 3) / -3 .

Example 6.27

Find the vector equation in parametric form and Cartesian equations of a straight passing through the points (−5, 7, −4) and (13, −5, 2) . Find the point where the straight line crosses the xy -plane.

Solution

The straight line passes through the points (−5, 7, −4) and (13, −5, 2) , and therefore, direction ratios of the straight line joining these two points are 18, −12, 6 . That is 3, −2,1.

So, the straight line is parallel to 3iˆ − 2 ˆj + kˆ . Therefore,

Required vector equation of the straight line in parametric form is  = (−5ˆi + 7 Ë†j âˆ’ 4ˆk ) + t(3ˆi âˆ’ 2ˆj + Ë†k ) or  = (13ˆi âˆ’ 5ˆj + 2ˆk ) + s(3ˆi âˆ’ 2ˆj +ˆk ) where s, t âˆˆ R.

Required cartesian equations of the straight line are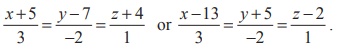 

An arbitrary point on the straight line is of the form

Since the straight line crosses the xy -plane, the z -coordinate of the point of intersection is zero.  Therefore, we have t − = 4 0 , that is, t = 4, and hence the straight line crosses the xy -plane at (7,−1,0).

Example 6.28

Find the angles between the straight line 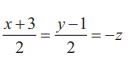 with coordinate axes.

Solution

If bˆ is a unit vector parallel to the given line, then bˆ = 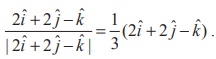 Therefore, from the definition of direction cosines of bˆ , we have

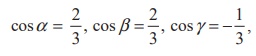
where α , β ,γ are the angles made by bˆ with the positive x -axis, positive y -axis, and positive z -axis, respectively. As the angle between the given straight line with the coordinate axes are same as the angles made by bˆ with the coordinate axes, we have α = cos-1 (2/3), β = cos-1( 2/3), γ = cos-1(-1/3), respectively.